题目内容
已知函数f(x),如果对任意一个三角形,只要它的三边长a,b,c都在f(x)的定义域内,就有f(a),f(b),f(c)也是某个三角形的三边长,则称f(x)为“保三角形函数”.在函数①f1(x)=| x |
分析:欲判断三个函数f(x)是不是“保三角形函数”,只须任给三角形,设它的三边长分别为a,b,c,则a+b>c,不妨假设a≤c,b≤c,我们判断f(a),f(b),f(c)是否满足任意两数之和大于第三个数,即任意两边之和大于第三边即可.
解答:解:f1(x),f2(x)是“保三角形函数”,f3(x)不是“保三角形函数”.
任给三角形,设它的三边长分别为a,b,c,则a+b>c,不妨假设a≤c,b≤c,
由于
+
>
>
>0,所以f1(x),f2(x)是“保三角形函数”.
对于f3(x),3,3,5可作为一个三角形的三边长,但32+32<52,
所以不存在三角形以32,32,52为三边长,故f3(x)不是“保三角形函数”.
故答案为:①②.
任给三角形,设它的三边长分别为a,b,c,则a+b>c,不妨假设a≤c,b≤c,
由于
| a |
| b |
| a+b |
| c |
对于f3(x),3,3,5可作为一个三角形的三边长,但32+32<52,
所以不存在三角形以32,32,52为三边长,故f3(x)不是“保三角形函数”.
故答案为:①②.
点评:要想判断f(x)为“保三角形函数”,要经过严密的论证说明f(x)满足“保三角形函数”的概念,但要判断f(x)不为“保三角形函数”,仅须要举出一个反例即可.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
 6、已知函数f(x)的导函数f′(x)=ax2+bx+c的图象如图,则f(x)的图象可能是( )
6、已知函数f(x)的导函数f′(x)=ax2+bx+c的图象如图,则f(x)的图象可能是( ) 已知函数f(x)=ax+b(a>0且a≠1)的图象如图所示,则a,b的值分别是( )
已知函数f(x)=ax+b(a>0且a≠1)的图象如图所示,则a,b的值分别是( ) 已知函数f(x)的定义域为[-1,5],部分对应值如下表.
已知函数f(x)的定义域为[-1,5],部分对应值如下表. (理)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
(理)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<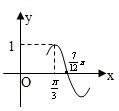 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则y=f(x)的图象可由函数g(x)=sinx的图象(纵坐标不变)( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则y=f(x)的图象可由函数g(x)=sinx的图象(纵坐标不变)( )