题目内容
某职业联赛的总决赛在甲、乙两队之间角逐，采用七场四胜制，即有一队胜四场，则此队获胜，且比赛结束．在每场比赛中，甲队获胜的概率是| 2 |
| 3 |
| 1 |
| 3 |
（Ⅰ）组织者在总决赛中获门票收入为120万元的概率是多少？
（Ⅱ）设ξ为组织者在总决赛中获得的门票收入数，求ξ的分布列．
分析：（1）门票收入为120万元这个事件包括打四场比赛，即甲连胜四场，乙连胜四场两个事件，且两个事件之间是互斥事件，列出结果．
（2）ξ为组织者在总决赛中获得的门票收入数，ξ的可能取值为120，150，180，210．算出各种情况对应的概率，写出分布列．
（2）ξ为组织者在总决赛中获得的门票收入数，ξ的可能取值为120，150，180，210．算出各种情况对应的概率，写出分布列．
解答：解：（Ⅰ）门票收入为120万元的概率：P1=(
)4+(
)4=
．
（Ⅱ）ξ的可能取值为120，150，180，210．
P(ξ=120)=
；
P(ξ=150)=
(
)3(
)×
+
(
)3(
)×
=
；
P(ξ=180)=
(
)3(
)2×
+
(
)3(
)2×
=
；
P(ξ=210)=
(
)3(
)3×
+
(
)3(
)3×
=
．
ξ的分布列为：
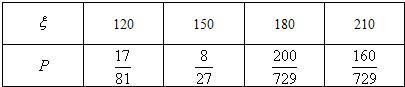
| 2 |
| 3 |
| 1 |
| 3 |
| 17 |
| 81 |
（Ⅱ）ξ的可能取值为120，150，180，210．
P(ξ=120)=
| 17 |
| 81 |
P(ξ=150)=
| C | 3 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 3 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 8 |
| 27 |
P(ξ=180)=
| C | 3 5 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 3 5 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 200 |
| 729 |
P(ξ=210)=
| C | 3 6 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 3 6 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 160 |
| 729 |
ξ的分布列为：
点评：归纳求离散型随机变量期望的步骤：①、确定离散型随机变量 的取值．②、写出分布列，并检查分布列的正确与否．③、求出期望．本题没有要求求出期望，同学们可以自己做出．
练习册系列答案
相关题目
，乙队获胜的概率是
，根据以往资料统计，每场比赛组织者可获门票收入为
万元，两队决出胜负后，问：
万元的概率是多少？
为组织者在总决赛中获得的门票收入数，求
，乙队获胜的概率是
，根据以往资料统计，每场比赛组织者可获门票收入为30万元，两队决出胜负后，问：
，乙队获胜的概率是
，根据以往资料统计，每场比赛组织者可获门票收入为30万元，两队决出胜负后，问：