题目内容
在锐角△ABC中,角A、B、C所对的边长分别为a、b、c,向量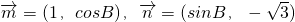 ,且
,且 .
.
(1)求角B的大小;
(2)若△ABC面积为 ,3ac=25-b2,求a,c的值.
,3ac=25-b2,求a,c的值.
解:(1)∵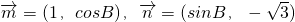
∴ =
=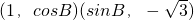 =
=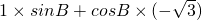 =
=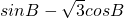
∵ ,∴
,∴
∴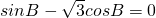 …(2分)
…(2分)
∵△ABC为锐角三角形,∴cosB≠0…(3分)
∴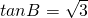 ,…(4分)
,…(4分)
∵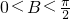
∴ .…(5分)
.…(5分)
(2)由b2=a2+c2-2accosB,得b2=a2+c2-ac,…(6分)
代入3ac=25-b2得3ac=25-a2-c2+ac,得a+c=5.…(7分)
∵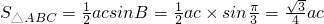 …(9分)
…(9分)
由题设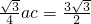 ,得ac=6…(10分)
,得ac=6…(10分)
联立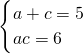 ,
,
解得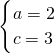 ,或
,或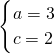 .…(12分)
.…(12分)
分析:(1)利用向量的数量积运算,根据向量垂直建立方程,即可求得角B的大小;
(2)利用余弦定理,三角形的面积公式,可得a,c的关系,解方程组,即可求得结论.
点评:本小题主要考查向量数量积、三角特殊值的运算,三角函数的基本关系,解三角形1等知识,考查化归与转化、方程的数学思想方法,以及运算求解能力.
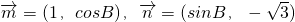
∴
 =
=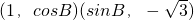 =
=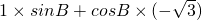 =
=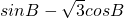
∵
 ,∴
,∴
∴
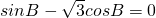 …(2分)
…(2分)∵△ABC为锐角三角形,∴cosB≠0…(3分)
∴
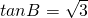 ,…(4分)
,…(4分)∵
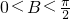
∴
 .…(5分)
.…(5分)(2)由b2=a2+c2-2accosB,得b2=a2+c2-ac,…(6分)
代入3ac=25-b2得3ac=25-a2-c2+ac,得a+c=5.…(7分)
∵
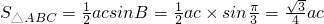 …(9分)
…(9分)由题设
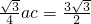 ,得ac=6…(10分)
,得ac=6…(10分)联立
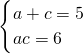 ,
,解得
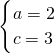 ,或
,或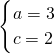 .…(12分)
.…(12分)分析:(1)利用向量的数量积运算,根据向量垂直建立方程,即可求得角B的大小;
(2)利用余弦定理,三角形的面积公式,可得a,c的关系,解方程组,即可求得结论.
点评:本小题主要考查向量数量积、三角特殊值的运算,三角函数的基本关系,解三角形1等知识,考查化归与转化、方程的数学思想方法,以及运算求解能力.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目