题目内容
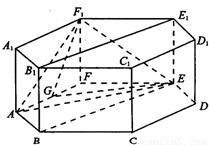
 已知正六棱柱ABCDEF-A1B1C1D1E1F1的所有棱长均为2,G为AF的中点.
已知正六棱柱ABCDEF-A1B1C1D1E1F1的所有棱长均为2,G为AF的中点.(1)求证:F1G∥平面BB1E1E;
(2)求证:平面F1AE⊥平面DEE1D1;
(3)求四面体EGFF1的体积.
分析:(1)根据AF∥BE,AF?平面BB1E1E,满足线面平行的判定定理,则AF∥平面BB1E1E,同理可证,AA1∥平面BB1E1E,根据面面平行的判定定理可知平面AA1F1F∥平面BB1E1E,又F1G?平面AA1F1F,根据面面平行的性质可知F1G∥平面BB1E1E;
(2)根据底面ABCDEF是正六边形,则AE⊥ED,又E1E⊥底面ABCDEF,所以E1E⊥AE,而E1E∩ED=E,根据线面垂直的判定定理可知
AE⊥平面DD1E1E,又AE?平面F1AE,最后根据面面垂直的判定定理可知平面F1AE⊥平面DEE1D1;
(3)根据F1F⊥底面FGE,则四面体EGFF1的高为F1F,然后利用三棱锥的体积公式进行求解即可.
(2)根据底面ABCDEF是正六边形,则AE⊥ED,又E1E⊥底面ABCDEF,所以E1E⊥AE,而E1E∩ED=E,根据线面垂直的判定定理可知
AE⊥平面DD1E1E,又AE?平面F1AE,最后根据面面垂直的判定定理可知平面F1AE⊥平面DEE1D1;
(3)根据F1F⊥底面FGE,则四面体EGFF1的高为F1F,然后利用三棱锥的体积公式进行求解即可.
解答:解:
(1)证明:因为AF∥BE,AF?平面BB1E1E,
所以AF∥平面BB1E1E,(2分)
同理可证,AA1∥平面BB1E1E,(3分)
所以,平面AA1F1F∥平面BB1E1E(4分)
又F1G?平面AA1F1F,所以F1G∥平面BB1E1E(5分)
(2)因为底面ABCDEF是正六边形,所以AE⊥ED,(7分)
又E1E⊥底面ABCDEF,所以E1E⊥AE,
因为E1E∩ED=E,所以AE⊥平面DD1E1E,(9分)
又AE?平面F1AE,所以平面F1AE⊥平面DEE1D1(10分)
(3)∵F1F⊥底面FGE,
VE-GFF1=VF1-GFE=
S△GEF•FF1=
×
×1×2sin120o×2=
(1)证明:因为AF∥BE,AF?平面BB1E1E,
所以AF∥平面BB1E1E,(2分)
同理可证,AA1∥平面BB1E1E,(3分)
所以,平面AA1F1F∥平面BB1E1E(4分)
又F1G?平面AA1F1F,所以F1G∥平面BB1E1E(5分)
(2)因为底面ABCDEF是正六边形,所以AE⊥ED,(7分)
又E1E⊥底面ABCDEF,所以E1E⊥AE,
因为E1E∩ED=E,所以AE⊥平面DD1E1E,(9分)
又AE?平面F1AE,所以平面F1AE⊥平面DEE1D1(10分)
(3)∵F1F⊥底面FGE,
VE-GFF1=VF1-GFE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 3 |
点评:本题主要考查直线与平面平行的判定,以及平面与平面垂直的判定和三棱锥的体积的计算,体积的求解在最近两年高考中频繁出现,值得重视.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 已知正六棱柱ABCDEF-A1B1C1D1E1F1的所有棱长均为2,G为AF的中点.
已知正六棱柱ABCDEF-A1B1C1D1E1F1的所有棱长均为2,G为AF的中点.