题目内容
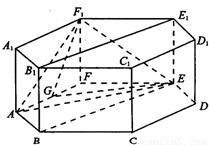
已知正六棱柱ABCDEF-A1B1C1D1E1F1的所有棱长均为2，G为AF的中点．（Ⅰ）求证：F1G∥平面BB1E1E；
（Ⅱ）求证：平面F1AE⊥平面DEE1D1；
（Ⅲ）求异面直线EG与F1A所成角的余弦值．
分析：（Ⅰ）利用平面AA1F1F与平面BB1E1E平行，来证明直线F1G∥平面BB1E1E即可．
（Ⅱ）先由AE⊥ED以及E1E⊥AE⇒AE⊥平面DD1E1E，就可得平面F1AE⊥平面DD1E1E．
（Ⅲ）利用底面ABCDEF是正六边形得EF⊥BF．建立如下图所示的空间直角坐标系，求出对应点的坐标以及
和
的坐标即可求出异面直线EG与F1A所成角的余弦值．
（Ⅱ）先由AE⊥ED以及E1E⊥AE⇒AE⊥平面DD1E1E，就可得平面F1AE⊥平面DD1E1E．
（Ⅲ）利用底面ABCDEF是正六边形得EF⊥BF．建立如下图所示的空间直角坐标系，求出对应点的坐标以及
| EG |
| F1A |
解答：证明：（Ⅰ）因为AF∥BE，AF?平面BB1E1E，
所以AF∥平面BB1E1E，
同理可证，AA1∥平面BB1E1E，
所以，平面AA1F1F∥平面BB1E1E
又F1G?平面AA1F1F，所以F1G∥平面BB1E1E
（Ⅱ）因为底面ABCDEF是正六边形，所以AE⊥ED，
又E1E⊥底面ABCDEF，所以E1E⊥AE，
因为E1E∩ED=E，所以AE⊥平面DD1E1E，
又AE?平面F1AE，所以平面F1AE⊥平面DD1E1E
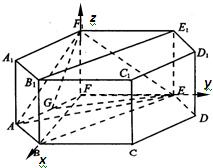（Ⅲ）由于底面ABCDEF是正六边形，
所以EF⊥BF．如图，
建立如图所示的空间直角坐标系．则
E（0，2，0），G（
，-
，0），F1（0，0，2），A（
，-1，0）．
则
=（
，-
，0），
=（
，-1，-2），
从而两异面直线EG与F1A所成角的余弦值为
cosθ=
=
=
所以AF∥平面BB1E1E，
同理可证，AA1∥平面BB1E1E，
所以，平面AA1F1F∥平面BB1E1E
又F1G?平面AA1F1F，所以F1G∥平面BB1E1E
（Ⅱ）因为底面ABCDEF是正六边形，所以AE⊥ED，
又E1E⊥底面ABCDEF，所以E1E⊥AE，
因为E1E∩ED=E，所以AE⊥平面DD1E1E，
又AE?平面F1AE，所以平面F1AE⊥平面DD1E1E
（Ⅲ）由于底面ABCDEF是正六边形，所以EF⊥BF．如图，
建立如图所示的空间直角坐标系．则
E（0，2，0），G（
| ||
| 2 |
| 1 |
| 2 |
| 3 |
则
| EG |
| ||
| 2 |
| 5 |
| 2 |
| F1A |
| 3 |
从而两异面直线EG与F1A所成角的余弦值为
cosθ=
| ||||
|
|
| 4 | ||||
|
| ||
| 7 |
点评：本题综合考查了面面垂直的判定以及线面平行的判定和异面直线所成角的三角函数值的求法，是对立体几何知识的综合考查．在证明线面平行时，一般转化为线线平行或面面平行来证．
练习册系列答案
相关题目
已知正六棱柱ABCDEF-A1B1C1D1E1F1的所有棱长均为2，G为AF的中点．
