题目内容
【题目】已知椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() .过原点
.过原点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 上的点,若
上的点,若![]() ,
, ![]() ,且
,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2) 设椭圆在点![]() 处的切线记为直线
处的切线记为直线![]() ,点
,点![]() 在
在![]() 上的射影分别为
上的射影分别为![]() ,过
,过![]() 作
作![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() ,试问
,试问![]() 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
【答案】(1) ![]() ;(2)1.
;(2)1.
【解析】试题分析; (1)设![]() ,则
,则![]() ,∴
,∴ ![]() ,设
,设![]() ,
, ![]() ,以及
,以及![]() ,
, ![]() ,由
,由![]() ,由椭圆的定义可得
,由椭圆的定义可得![]() ,结合
,结合![]() ,综合
,综合![]() 可得:
可得: ![]() ,可得椭圆
,可得椭圆![]() 的方程;
的方程;
(2)由(1)知![]() ,直线
,直线![]() 的方程为:
的方程为: ![]() ,由此可得
,由此可得
![]() .,又∵
.,又∵![]() ,∴
,∴ ![]() 的方程为
的方程为![]() ,可得
,可得![]()
则可得![]() ,又
,又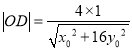 ,∴
,∴ ![]() .,故
.,故![]() .
.
当直线![]() 平行于
平行于![]() 轴时,易知
轴时,易知![]() ,结论显然成立.
,结论显然成立.
综上,可知![]() 为定值1.
为定值1.
试题解析:(1)设![]() ,则
,则![]() ,∴
,∴![]() ,设
,设![]() ,由
,由![]() ,
,
![]() ,将
,将![]() 代入
代入![]() ,整体消元得:
,整体消元得:
![]() ,∴
,∴![]()
由![]() ,且
,且 ![]() ,∴
,∴ ![]() ,
,
由椭圆的对称性知![]() ,
,
有![]() ,则
,则![]()
∵![]() ,综合
,综合![]() 可得:
可得: ![]()
∴椭圆![]() 的方程为:
的方程为: ![]() .
.
(2)由(1)知,直线![]() 的方程为:
的方程为: ![]()
即: ![]() ,所以
,所以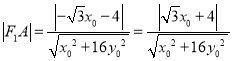
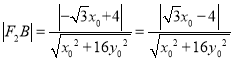
∴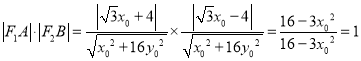 .
.
∵![]() ,∴
,∴ ![]() 的方程为
的方程为![]() ,令
,令![]() ,可得
,可得![]() ,∴
,∴ ![]()
则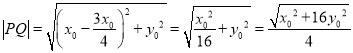
又点![]() 到直线
到直线![]() 的距离为
的距离为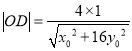 ,∴
,∴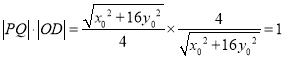 .
.
∴![]() .
.
当直线![]() 平行于
平行于![]() 轴时,易知
轴时,易知![]() ,结论显然成立.
,结论显然成立.
综上, ![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目