题目内容
(本小题满分12分)
已知函数y=4cos2x-4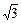 sinxcosx-1(x∈R).
sinxcosx-1(x∈R).
(1)求出函数的最小正周期;
(2)求出函数的最大值及其相对应的x值;
(3)求出函数的单调增区间;
(4)求出函数的对称轴。
已知函数y=4cos2x-4
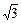 sinxcosx-1(x∈R).
sinxcosx-1(x∈R).(1)求出函数的最小正周期;
(2)求出函数的最大值及其相对应的x值;
(3)求出函数的单调增区间;
(4)求出函数的对称轴。
略
解:y=4cos2x-4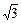 sinxcosx-1=4×
sinxcosx-1=4×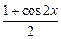 -4
-4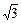 sinxcosx-1 ……………1分
sinxcosx-1 ……………1分
=2cos2x-2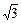 sin2x+1=4(
sin2x+1=4(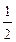 cos2x-
cos2x-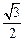 sin2x)+1 ………………2分
sin2x)+1 ………………2分
=4cos(2x+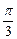 )+1 ………………4分
)+1 ………………4分
(1)T=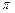 ………………6分
………………6分
(2)当cos(2x+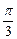 )=1时,y最大值=5,此时2x+
)=1时,y最大值=5,此时2x+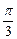 =2kπ,x=kπ-
=2kπ,x=kπ- (k∈Z)
(k∈Z)
………………8分
(3)令-π+2kπ≤2x+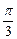 ≤2kπ,得-
≤2kπ,得-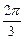 +kπ≤x≤-
+kπ≤x≤- +kπ, ………………9分
+kπ, ………………9分
∴函数的单调递增区间是[-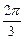 +kπ,-
+kπ,- +kπ](k∈Z) ………………10分
+kπ](k∈Z) ………………10分
(4)令2x+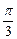 =kπ,得x=
=kπ,得x=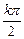 -
- ………………11分
………………11分
∴对称轴方程为x=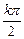 -
- (k∈Z) ………………12分
(k∈Z) ………………12分
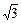 sinxcosx-1=4×
sinxcosx-1=4×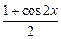 -4
-4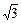 sinxcosx-1 ……………1分
sinxcosx-1 ……………1分=2cos2x-2
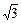 sin2x+1=4(
sin2x+1=4(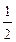 cos2x-
cos2x-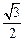 sin2x)+1 ………………2分
sin2x)+1 ………………2分=4cos(2x+
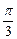 )+1 ………………4分
)+1 ………………4分(1)T=
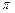 ………………6分
………………6分(2)当cos(2x+
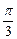 )=1时,y最大值=5,此时2x+
)=1时,y最大值=5,此时2x+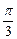 =2kπ,x=kπ-
=2kπ,x=kπ- (k∈Z)
(k∈Z)………………8分
(3)令-π+2kπ≤2x+
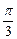 ≤2kπ,得-
≤2kπ,得-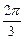 +kπ≤x≤-
+kπ≤x≤- +kπ, ………………9分
+kπ, ………………9分∴函数的单调递增区间是[-
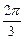 +kπ,-
+kπ,- +kπ](k∈Z) ………………10分
+kπ](k∈Z) ………………10分(4)令2x+
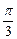 =kπ,得x=
=kπ,得x=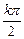 -
- ………………11分
………………11分∴对称轴方程为x=
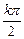 -
- (k∈Z) ………………12分
(k∈Z) ………………12分
练习册系列答案
相关题目
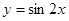 的图像平移后得到函数
的图像平移后得到函数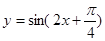 的图像,则下面说法正确的是
的图像,则下面说法正确的是 
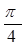
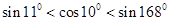
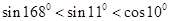


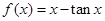 在区间
在区间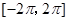 上的零点个数是 ( )
上的零点个数是 ( )
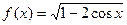 的定义域是________________________
的定义域是________________________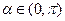 ,向量
,向量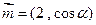 ,
,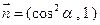 ,且
,且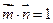 ,
,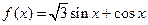 。
。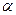 的大小;(Ⅱ)求函数
的大小;(Ⅱ)求函数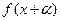 的单调递减区间。
的单调递减区间。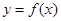 的图象按向量
的图象按向量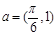 平移后得到函数
平移后得到函数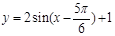 的图象,则函数
的图象,则函数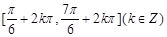
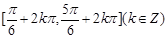
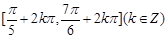
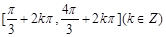
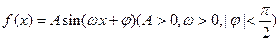 的部分图象如图所示。
的部分图象如图所示。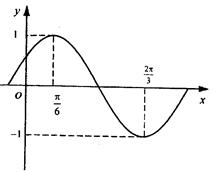
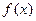 的最小正周期及解析式;
的最小正周期及解析式;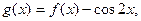 求函数
求函数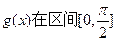 上的最大值和最小值
上的最大值和最小值