题目内容
3. 如图,△ABC中,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.
如图,△ABC中,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.(1)求证:O、B、D、E四点共圆;
(2)求证:AB+AC=$\frac{2D{E}^{2}}{DM}$.
分析 (1)连接BE、OE,由直径所对的圆周角为直角,得到BE⊥EC,从而得出DE=BD=$\frac{1}{2}$BC,由此证出△ODE≌△ODB,得∠OED=∠OBD=90°,利用圆内接四边形形的判定定理得到O、B、D、E四点共圆;
(2)延长DO交圆O于点H,由(1)的结论证出DE为圆O的切线,从而得出DE2=DM•DH,再将DH分解为DO+OH,并利用OH=$\frac{1}{2}$AB和DO=$\frac{1}{2}$AC,化简即可得到等式2DE2=DM•AC+DM•AB成立,即可证明结论.
解答 解:(1)连接BE、OE,则
∵AB为圆0的直径,∴∠AEB=90°,得BE⊥EC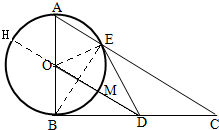 ,
,
又∵D是BC的中点,
∴ED是Rt△BEC的中线,可得DE=BD.
又∵OE=OB,OD=OD,∴△ODE≌△ODB.
可得∠OED=∠OBD=90°,
因此,O、B、D、E四点共圆;
(2)延长DO交圆O于点H,
∵DE⊥OE,OE是半径,∴DE为圆O的切线.
可得DE2=DM•DH=DM•(DO+OH)=DM•DO+DM•OH.
∵OH=$\frac{1}{2}$AB,OD为△ABC的中位线,得DO=$\frac{1}{2}$AC,
∴DE2=DM•$\frac{1}{2}$AC+DM•$\frac{1}{2}$AB,化简得2DE2=DM•AC+DM•AB,
∴AB+AC=$\frac{2D{E}^{2}}{DM}$.
点评 本题着重考查了圆的切线的性质定理与判定、直径所对的圆周角、全等三角形的判定与性质等知识,属于中档题.

练习册系列答案
相关题目
11.如图,在△OAB中,P为线段AB上的一点,$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,且$\overrightarrow{BP}$=3$\overrightarrow{PA}$,则( )


| A. | x=$\frac{1}{4}$,y=$\frac{3}{4}$ | B. | x=$\frac{1}{3}$,y=$\frac{2}{3}$ | C. | x=$\frac{3}{4}$,y=$\frac{1}{4}$ | D. | x=$\frac{2}{3}$,y=$\frac{1}{3}$ |
 已知如图1所示的四边形ABCD中,DA⊥AB,点E为AD中点,连接CE,AD=EC=2AB=$\sqrt{2}$BC=2;现将四边形沿着CE进行翻折,使得平面CDE⊥平面ABCE,连接DA,DB,BE得到如图2所示的四棱锥D-ABCE.
已知如图1所示的四边形ABCD中,DA⊥AB,点E为AD中点,连接CE,AD=EC=2AB=$\sqrt{2}$BC=2;现将四边形沿着CE进行翻折,使得平面CDE⊥平面ABCE,连接DA,DB,BE得到如图2所示的四棱锥D-ABCE.