题目内容
求证：双曲线
=1(a＞0，b＞0)上任何一点到两条渐近线的距离之积为定值.
思路分析：本题考查双曲线几何性质的综合应用.将双曲线有关的性质综合起来在解题中综合考查，对于这类问题，我们要有良好的基本功才能对付好.
证明：设P(x0，y0)是双曲线上任意一点，由双曲线的两条渐近线方程为bx+ay=0和bx-ay=0可得：P到bx+ay=0的距离d1=;
P到bx-ay=0的距离d2=
.
∴d1·d2=
·
=
.
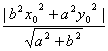又P在双曲线上，∴
=1
,即b2x02-a2y02=a2b2.∴d1·d2=
，即点P到两条渐近线的距离之积为定值.
方法归纳 所谓定值，是与P点在曲线上的位置无关，为了达到目标明确，可先通过特殊的情况求出一个常数，猜想其定值.
练习册系列答案
相关题目
已知双曲线
=1(a＞0,b＞0)的动弦BC平行于虚轴，M、N是双曲线的左、右顶点,
=1(a＞0,b＞0)的动弦BC平行于虚轴，M、N是双曲线的左、右顶点,(1)求直线MB、CN的交点P的轨迹方程；
(2)若P(x1,y1)，B(x2,y2),求证:a是x1、x2的比例中项.
=1(a＞0,b＞0)的动弦BC平行于虚轴，M、N是双曲线的左、右顶点,
-
=1(a>0,b>0)上任何一点到两条渐近线的距离之积为定值.
=1(a＞0,b＞0)上任何一点到两条渐近线的距离之积为定值.