题目内容
12. 如图,正方体ABCD-A1B1C1D1的棱长为2,P为棱CD上的一点,且三棱锥A-CPD1的体积为$\frac{2}{3}$.
如图,正方体ABCD-A1B1C1D1的棱长为2,P为棱CD上的一点,且三棱锥A-CPD1的体积为$\frac{2}{3}$.(1)求CP的长;
(2)求直线AD与平面APD1所成的角θ的正弦值;
(3)请直接写出正方体的棱上满足C1M∥平面APD1的所有点M的位置,并任选其中的一点予以证明.
分析 (1)根据三棱锥的等积法求解得出$\frac{1}{3}×2×\frac{1}{2}×CP$×2=$\frac{2}{3}$,求解即可得出CP,
(2)距离坐标系得出$\overrightarrow{AD}$=(0,2,0),$\overrightarrow{AP}$=(1,2,0),$\overrightarrow{A{D}_{1}}$=(0,2,2),运用向量的数量积得出法向量$\overrightarrow{n}$=(2,-1,1),sinθ=$\frac{|\overrightarrow{AD}•\overrightarrow{n}|}{|\overrightarrow{AD}|•\overrightarrow{|n|}}$,
(3)判断M点的位置为A1B1中点,平面APD1的一个法向量为$\overrightarrow{n}$=(2,-1,1),运用直线与平面的平行的判定定理得出C1M∥平面APD1.
解答 解:(1)依题意得,AD⊥平面CPD, AD=DD1=2,
AD=DD1=2,
所以三棱锥A-CPD1的体积为$\frac{1}{3}×2×\frac{1}{2}×CP$×2=$\frac{2}{3}$,
CP=1,
(2)以A为原点,AB,AD,AA1,所在直线分别为x,y,z轴,建立坐标系,
A(0,0,0),D(0,2,0),P(1.2,0),D1(0,2,2),
$\overrightarrow{AD}$=(0,2,0),$\overrightarrow{AP}$=(1,2,0),$\overrightarrow{A{D}_{1}}$=(0,2,2),
设平面APD1的一个法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{AP}•\overrightarrow{n}=0}\\{\overrightarrow{AD}•\overrightarrow{n}=0}\end{array}\right.$
∴$\left\{\begin{array}{l}{x+2y=0}\\{2y+2z=0}\end{array}\right.$得出$\left\{\begin{array}{l}{x=2}\\{y=-1}\\{z=1}\end{array}\right.$
∴$\overrightarrow{n}$=(2,-1,1),
即sinθ=$\frac{|\overrightarrow{AD}•\overrightarrow{n}|}{|\overrightarrow{AD}|•\overrightarrow{|n|}}$=$\frac{2}{2×\sqrt{6}}$=$\frac{\sqrt{6}}{6}$,
故直线AD与平面APD1所成的角θ的正弦值为$\frac{\sqrt{6}}{6}$.
(3)∵M点的位置为A1B1中点,
可知C1(2,2,2),M(1,0,2),$\overrightarrow{{C}_{1}M}$=(-1,-2,0),
∴平面APD1的一个法向量为$\overrightarrow{n}$=(2,-1,1),
∴$\overrightarrow{{C}_{1}M}$$•\overrightarrow{n}$=0,
∵C1M?平面APD1,
∴C1M∥平面APD1
点评 本题考查了直线与平面所成的角,运用平面的法向量,结合向量的运用求解夹角,证明平行问题,属于有点计算能力的证明题目.

| A. | 840种 | B. | 5040种 | C. | 140种 | D. | 1680种 |
| A. | $\frac{5}{12}$ | B. | $\frac{7}{12}$ | C. | $\frac{7}{18}$ | D. | $\frac{7}{9}$ |
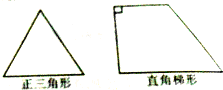 用斜二测画法画出下列水平放置图形的直观图.
用斜二测画法画出下列水平放置图形的直观图. 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其中F1,F2为左、右焦点,且离心率e=$\frac{\sqrt{3}}{3}$,直线l与椭圆交于两不同点P(x1,y1),Q(x2,y2).当直线l过椭圆C右焦点F2且倾斜角为$\frac{π}{4}$时,原点O到直线l的距离为$\frac{\sqrt{2}}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其中F1,F2为左、右焦点,且离心率e=$\frac{\sqrt{3}}{3}$,直线l与椭圆交于两不同点P(x1,y1),Q(x2,y2).当直线l过椭圆C右焦点F2且倾斜角为$\frac{π}{4}$时,原点O到直线l的距离为$\frac{\sqrt{2}}{2}$.