题目内容
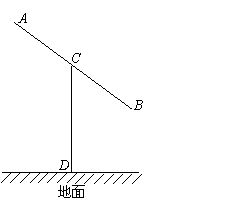
某建筑的金属支架如图所示,根据要求AB至少长2.8m,C为AB的中点,B到D的距离比CD的长小0.5m,∠BCD=60°,已知建筑支架的材料每米的价格一定,问怎样设计AB,CD的长,可使建造这个支架的成本最低?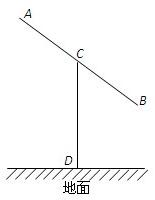
分析:通过三角形中的余弦定理得到a,b的等量关系;通过换元转化成积是定值;求和的最小值问题;再利用基本不等式解.
解答:解:设BC=am(a≥1,4),CD=bm.连接BD.则BD=b-
则在△CDB中,(b-
)2=b2+a2-2abcos60°,
∴b=
,
∴b+2a=
+2a,
设t=a-1,t≥
-1=0.4,
则b+2a=
+2(t+1)=3t+
+4≥7,
等号成立时t=0.5>0.4,a=1.5,b=4.
答:当AB=3m,CD=4m时,建造这个支架的成本最低.
| 1 |
| 2 |
则在△CDB中,(b-
| 1 |
| 2 |
∴b=
a2-
| ||
| a-1 |
∴b+2a=
a2-
| ||
| a-1 |
设t=a-1,t≥
| 2.8 |
| 2 |
则b+2a=
(t+1)2-
| ||
| t |
| 3 |
| 4t |
等号成立时t=0.5>0.4,a=1.5,b=4.
答:当AB=3m,CD=4m时,建造这个支架的成本最低.
点评:本题考查解三角形;数学上的换元思想;用基本不等式求函数最值.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目


 某建筑的金属支架如图所示,根据要求
某建筑的金属支架如图所示,根据要求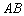 至少长2.8m,
至少长2.8m,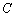 为
为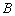 到
到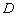 的距离比
的距离比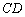 的长小0.5m,
的长小0.5m,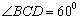 ,已知建筑支架的材料每米的价格一定,问怎样设计
,已知建筑支架的材料每米的价格一定,问怎样设计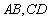 的长,可使建造这个支架的成本最低?
的长,可使建造这个支架的成本最低?