题目内容
选修4-5:不等式选讲
已知函数x>0,y>0,z>0,求证:
(Ⅰ)x3+y3≥x2y+xy2;
(Ⅱ)x3+y3+z3≥x2•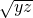 +y2•
+y2•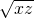 +z2•
+z2• .
.
证明:(Ⅰ)x3+y3-x2y-xy2=(x-y)(x2-y2)=(x-y)2(x+y)…(2分)
∵x>0,y>0,(x-y)2≥0,…(4分)
∴x3+y3≥x2y+xy2;…(5分)
(Ⅱ)由(Ⅰ)x3+y3≥x2y+xy2;同理z3+y3≥z2y+zy2;x3+z3≥x2z+xz2,…(6分)
∴2(x3+y3+z3)≥x2(y+z)+y2(z+x)+z2(x+y)≥2(x2•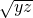 +y2•
+y2•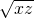 +z2•
+z2• ).
).
∴x3+y3+z3≥x2•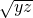 +y2•
+y2•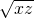 +z2•
+z2• . …(10分)
. …(10分)
分析:(Ⅰ)作差,因式分解,即可证得结论;
(Ⅱ)由(Ⅰ)x3+y3≥x2y+xy2;同理z3+y3≥z2y+zy2;x3+z3≥x2z+xz2,三式相加,利用基本不等式,即可得解.
点评:本题考查不等式的证明,考查作差比较法,考查基本不等式的运用,选择正确的方法是关键.
∵x>0,y>0,(x-y)2≥0,…(4分)
∴x3+y3≥x2y+xy2;…(5分)
(Ⅱ)由(Ⅰ)x3+y3≥x2y+xy2;同理z3+y3≥z2y+zy2;x3+z3≥x2z+xz2,…(6分)
∴2(x3+y3+z3)≥x2(y+z)+y2(z+x)+z2(x+y)≥2(x2•
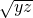 +y2•
+y2•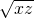 +z2•
+z2• ).
).∴x3+y3+z3≥x2•
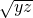 +y2•
+y2•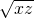 +z2•
+z2• . …(10分)
. …(10分)分析:(Ⅰ)作差,因式分解,即可证得结论;
(Ⅱ)由(Ⅰ)x3+y3≥x2y+xy2;同理z3+y3≥z2y+zy2;x3+z3≥x2z+xz2,三式相加,利用基本不等式,即可得解.
点评:本题考查不等式的证明,考查作差比较法,考查基本不等式的运用,选择正确的方法是关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目