题目内容
11.已知正△ABC三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点E是线段AB的中点,过点E作球O的截面,则截面面积的最小值是$\frac{9π}{4}$.分析 设正△ABC的中心为O1,连结O1O、O1C、O1E、OE.根据球的截面圆性质、正三角形的性质与勾股定理,结合题中数据算出OE.而经过点E的球O的截面,当截面与OE垂直时截面圆的半径最小,相应地截面圆的面积有最小值,由此算出截面圆半径的最小值,从而可得截面面积的最小值.
解答 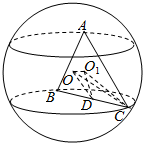 解:设正△ABC的中心为O1,连结O1O、O1C、O1E、OE,
解:设正△ABC的中心为O1,连结O1O、O1C、O1E、OE,
∵O1是正△ABC的中心,A、B、C三点都在球面上,
∴O1O⊥平面ABC,结合O1C?平面ABC,可得O1O⊥O1C,
∵球的半径R=2,球心O到平面ABC的距离为1,得O1O=1,
∴Rt△O1OC中,O1C=$\sqrt{{R}^{2}-{{OO}_{1}}^{2}}$=$\sqrt{3}$.
又∵E为AB的中点,∴正△ABC中,O1E=$\frac{1}{2}$O1C=$\frac{\sqrt{3}}{2}$.
∴Rt△OO1E中,OE=$\sqrt{{{O}_{1}E}^{2}+{{OO}_{1}}^{2}}$=$\sqrt{\frac{3}{4}+1}$=$\frac{\sqrt{7}}{2}$.
∵过E作球O的截面,当截面与OE垂直时,截面圆的半径最小,
∴当截面与OE垂直时,截面圆的面积有最小值.
此时截面圆的半径r=$\sqrt{{R}^{2}-{{EO}_{1}}^{2}}$=$\sqrt{{2}^{2}-({\frac{\sqrt{7}}{2})}^{2}}$=$\frac{3}{2}$,
可得截面面积为S=πr2=$\frac{9π}{4}$.
故答案为:$\frac{9π}{4}$.
点评 本题已知球的内接正三角形与球心的距离,求经过正三角形中点的最小截面圆的面积.着重考查了勾股定理、球的截面圆性质与正三角形的性质等知识,属于中档题.

 黄冈创优卷系列答案
黄冈创优卷系列答案