题目内容
已知函数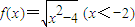 ,记f-1(x)为f(x)的反函数,若数列{an}满足a1=1,an+1=-f-1(an)(n∈N*).
,记f-1(x)为f(x)的反函数,若数列{an}满足a1=1,an+1=-f-1(an)(n∈N*).(1)求数列{an}的通项公式;
(2)设
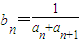 ,问:是否存在常数k,使得对任意的正整数n都有b1+b2+…+bn≤k•n成立.若存在,求出常数k的取值范围;若不存在,请说明理由.
,问:是否存在常数k,使得对任意的正整数n都有b1+b2+…+bn≤k•n成立.若存在,求出常数k的取值范围;若不存在,请说明理由.
【答案】分析:(1)由函数y= ,得
,得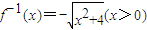 ,根据题意和反函数定义可得:an2-an-12=4,a1=1,由此能够求出
,根据题意和反函数定义可得:an2-an-12=4,a1=1,由此能够求出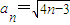 ,n∈N*.
,n∈N*.
(2)由 ,知
,知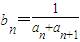 =
= =
= ,b1+b2+…+bn=
,b1+b2+…+bn= .对任意的正整数n都有b1+b2+…+bn≤k•n成立,所以对任意的正整数n都有
.对任意的正整数n都有b1+b2+…+bn≤k•n成立,所以对任意的正整数n都有 ≤k•n成立.整理,得:对任意的正整数n都有16nk2+8k-4≥0成立,由此能求出k的取值范围.
≤k•n成立.整理,得:对任意的正整数n都有16nk2+8k-4≥0成立,由此能求出k的取值范围.
解答:解:(1)∵函数y= ,
,
∴y2=x2-4,y>0,
 ,x,y互换,得
,x,y互换,得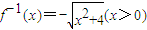 ,
,
根据题意和反函数定义可得:an2-an-12=4,a1=1,
∴an2=1+4(n-1)=4n-3,n∈N*,
∴ ,n∈N*.
,n∈N*.
(2)∵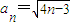 ,n∈N*,
,n∈N*,
∴ =
=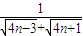 =
= ,
,
∴b1+b2+…+bn=
 )]
)]
= .
.
∵对任意的正整数n都有b1+b2+…+bn≤k•n成立,
∴对任意的正整数n都有 ≤k•n成立.
≤k•n成立.
整理,得:对任意的正整数n都有16nk2+8k-4≥0成立,
∵对任意的正整数n都有16nk2≥0,
∴8k-4≥0,k 时,对任意的正整数n都有b1+b2+…+bn≤k•n成立.
时,对任意的正整数n都有b1+b2+…+bn≤k•n成立.
故存在常数k,k的取值范围[ +∞).
+∞).
点评:本题考查数列与函数的综合,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.
 ,得
,得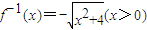 ,根据题意和反函数定义可得:an2-an-12=4,a1=1,由此能够求出
,根据题意和反函数定义可得:an2-an-12=4,a1=1,由此能够求出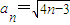 ,n∈N*.
,n∈N*.(2)由
 ,知
,知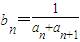 =
= =
= ,b1+b2+…+bn=
,b1+b2+…+bn= .对任意的正整数n都有b1+b2+…+bn≤k•n成立,所以对任意的正整数n都有
.对任意的正整数n都有b1+b2+…+bn≤k•n成立,所以对任意的正整数n都有 ≤k•n成立.整理,得:对任意的正整数n都有16nk2+8k-4≥0成立,由此能求出k的取值范围.
≤k•n成立.整理,得:对任意的正整数n都有16nk2+8k-4≥0成立,由此能求出k的取值范围.解答:解:(1)∵函数y=
 ,
,∴y2=x2-4,y>0,
 ,x,y互换,得
,x,y互换,得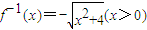 ,
,根据题意和反函数定义可得:an2-an-12=4,a1=1,
∴an2=1+4(n-1)=4n-3,n∈N*,
∴
 ,n∈N*.
,n∈N*.(2)∵
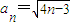 ,n∈N*,
,n∈N*,∴
 =
=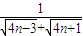 =
= ,
,∴b1+b2+…+bn=

 )]
)]=
 .
.∵对任意的正整数n都有b1+b2+…+bn≤k•n成立,
∴对任意的正整数n都有
 ≤k•n成立.
≤k•n成立.整理,得:对任意的正整数n都有16nk2+8k-4≥0成立,
∵对任意的正整数n都有16nk2≥0,
∴8k-4≥0,k
 时,对任意的正整数n都有b1+b2+…+bn≤k•n成立.
时,对任意的正整数n都有b1+b2+…+bn≤k•n成立.故存在常数k,k的取值范围[
 +∞).
+∞).点评:本题考查数列与函数的综合,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
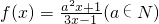 ,方程f(x)=-2x+7有两个根x1,x2,且x1<1<x2<3.
,方程f(x)=-2x+7有两个根x1,x2,且x1<1<x2<3.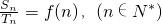 ,设
,设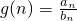 ,求g(n)的解析式及g(n)的最大值;
,求g(n)的解析式及g(n)的最大值; ,方程f(x)=-2x+7有两个根x1,x2,且x1<1<x2<3.
,方程f(x)=-2x+7有两个根x1,x2,且x1<1<x2<3. ,设
,设 ,求g(n)的解析式及g(n)的最大值;
,求g(n)的解析式及g(n)的最大值;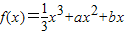 ,且f'(-1)=0
,且f'(-1)=0 ,且f'(-1)=0
,且f'(-1)=0