题目内容
已知一次函数y=ax+b的图象不经过第一象限,且在区间[-2,1]上的最大值和最小值分别是1和-2,求函数f(x)=x2-ax+b在[-2,1]上的最大值和最小值.分析:由题意可得:a<0,b≤0;再根据一次函数的最大值和最小值得到a=-1,b=-1,进而再结合二次函数的有关性质求出二次函数的最值.
解答:解:因为y=ax+b的图象不经过第一象限,因此a<0,b≤0;
又因为函数y=ax+b在区间[-2,1]上的最大值和最小值分别是1和-2,
所以可得:
,解得:a=-1,b=-1,
所以函数f(x)=x2+x-1,
所以函数f(x)的对称轴x=-
<0.
根据二次函数的性质可得:函数f(x)在[-2,1]上的最大值和最小值分别为1,-
.
又因为函数y=ax+b在区间[-2,1]上的最大值和最小值分别是1和-2,
所以可得:
|
所以函数f(x)=x2+x-1,
所以函数f(x)的对称轴x=-
| 1 |
| 2 |
根据二次函数的性质可得:函数f(x)在[-2,1]上的最大值和最小值分别为1,-
| 5 |
| 4 |
点评:本题考查二次函数和一次函数的概念,以及一次函数与二次函数的有关性质.

练习册系列答案
相关题目
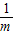 +
+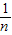 的最小值为 .
的最小值为 .