题目内容
某省环保研究所对市中心每天环境放射性污染情况进行调查研究后,发现一天中环境综合放射性污染指数f(x)与时刻x(时) 的关系为f(x)=|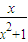 -a|+2a+
-a|+2a+ ,x∈[0,24],其中a是与气象有关的参数,且a∈[0,
,x∈[0,24],其中a是与气象有关的参数,且a∈[0, ].
].(1)令t=
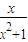 ,x∈[0,24],写出该函数的单调区间,并选择其中一种情形进行证明;
,x∈[0,24],写出该函数的单调区间,并选择其中一种情形进行证明;(2)若用每天f(x)的最大值作为当天的综合放射性污染指数,并记作M(a),求M(a);
(3)省政府规定,每天的综合放射性污染指数不得超过2,试问目前市中心的综合放射性污染指数M(a)是否超标?
【答案】分析:(1)单调递增区间为[0,1];单调递减区间为[1,24],利用单调性的定义可以证明;
(2)先确定t的取值范围是[0, ],再进行分类讨论,从而可得M(a)的解析式;
],再进行分类讨论,从而可得M(a)的解析式;
(3)利用分段函数,可得当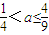 时不超标,从而可得结论.
时不超标,从而可得结论.
解答:解:(1)单调递增区间为[0,1];单调递减区间为[1,24].
证明:任取0≤x1<x2≤1,t(x1)-t(x2)=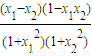 ,
,
∵0≤x1<x2≤1,∴x1-x2<0,1-x1x2>0,∴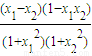 <0,∴t(x1)-t(x2)<0.
<0,∴t(x1)-t(x2)<0.
所以函数t(x)在[0,1]上为增函数.(同理可证在区间[1,24]单调递减)
(2)由函数的单调性知tmax(x)=t(1)=1,tmin(x)=t(0)=0,
∴t=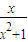 =
=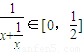 ,∴t的取值范围是[0,
,∴t的取值范围是[0, ].
].
当a∈[0, ]时,由于f(x)=|
]时,由于f(x)=|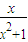 -a|+2a+
-a|+2a+ ,则可记g(t)=|t-a|+2a+
,则可记g(t)=|t-a|+2a+
则g(t)=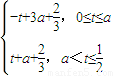
∵g(t)在[0,a]上单调递减,在(a, ]上单调递增,
]上单调递增,
且g(0)=3a+ .g(
.g( )=a+
)=a+
∴g(0)-g( )=2(a-
)=2(a- ).
).
故M(a)=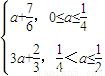 .
.
(3)当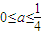 时,
时,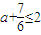 ,∴
,∴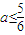 ,不满足题意;
,不满足题意;
当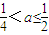 时,
时,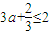 ,∴a≤
,∴a≤ ,∴
,∴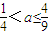 时,满足题意
时,满足题意
故当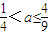 时不超标,当
时不超标,当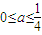 时超标.
时超标.
点评:本题主要考查了函数模型的选择与应用、考查求函数解析式及分类讨论的思想,属于实际应用题.
(2)先确定t的取值范围是[0,
 ],再进行分类讨论,从而可得M(a)的解析式;
],再进行分类讨论,从而可得M(a)的解析式;(3)利用分段函数,可得当
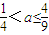 时不超标,从而可得结论.
时不超标,从而可得结论.解答:解:(1)单调递增区间为[0,1];单调递减区间为[1,24].
证明:任取0≤x1<x2≤1,t(x1)-t(x2)=
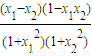 ,
,∵0≤x1<x2≤1,∴x1-x2<0,1-x1x2>0,∴
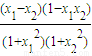 <0,∴t(x1)-t(x2)<0.
<0,∴t(x1)-t(x2)<0.所以函数t(x)在[0,1]上为增函数.(同理可证在区间[1,24]单调递减)
(2)由函数的单调性知tmax(x)=t(1)=1,tmin(x)=t(0)=0,
∴t=
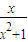 =
=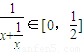 ,∴t的取值范围是[0,
,∴t的取值范围是[0, ].
].当a∈[0,
 ]时,由于f(x)=|
]时,由于f(x)=|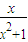 -a|+2a+
-a|+2a+ ,则可记g(t)=|t-a|+2a+
,则可记g(t)=|t-a|+2a+
则g(t)=
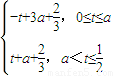
∵g(t)在[0,a]上单调递减,在(a,
 ]上单调递增,
]上单调递增,且g(0)=3a+
 .g(
.g( )=a+
)=a+
∴g(0)-g(
 )=2(a-
)=2(a- ).
).故M(a)=
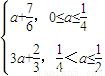 .
.(3)当
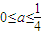 时,
时,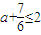 ,∴
,∴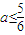 ,不满足题意;
,不满足题意;当
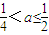 时,
时,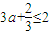 ,∴a≤
,∴a≤ ,∴
,∴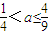 时,满足题意
时,满足题意故当
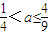 时不超标,当
时不超标,当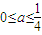 时超标.
时超标.点评:本题主要考查了函数模型的选择与应用、考查求函数解析式及分类讨论的思想,属于实际应用题.

练习册系列答案
相关题目
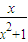 -a|+2a+
-a|+2a+ ,x∈[0,24],其中a是与气象有关的参数,且a∈[0,
,x∈[0,24],其中a是与气象有关的参数,且a∈[0, ].
].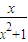 ,x∈[0,24],写出该函数的单调区间,并选择其中一种情形进行证明;
,x∈[0,24],写出该函数的单调区间,并选择其中一种情形进行证明;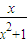 -a|+2a+
-a|+2a+ ,x∈[0,24],其中a是与气象有关的参数,且a∈[0,
,x∈[0,24],其中a是与气象有关的参数,且a∈[0, ].
].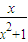 ,x∈[0,24],写出该函数的单调区间,并选择其中一种情形进行证明;
,x∈[0,24],写出该函数的单调区间,并选择其中一种情形进行证明;