题目内容
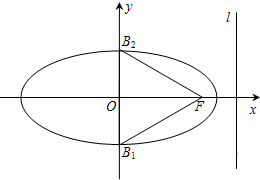 点B1,B2是椭圆
点B1,B2是椭圆| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆方程;
(2)求经过点O、F且与右准线l相切的圆的方程.
分析:(1)可得OF=c,OB2=b,B2F=a,可得离心率和准线方程,解方程组可得ab的值,可得方程;
(2)可得右准线方程为x=4,由题意可设圆心D(
, m),半径为
,可得圆的方程,代入点O(0,0)可的m的方程,解之可得答案.
(2)可得右准线方程为x=4,由题意可设圆心D(
| 3 |
| 2 |
| 5 |
| 2 |
解答: 解:(1)因为△B1B2F为正三角形,OF=c,OB2=b,B2F=a,
解:(1)因为△B1B2F为正三角形,OF=c,OB2=b,B2F=a,
所以e=
=
=cos30°=
.…(3分)
准线l的方程:x=
,
所以
解之得
…(6分)
于是b=
.
故椭圆方程为
+
=1.…(7分)
(2)设所求圆的圆心为D,由(1)知椭圆的右准线方程为x=4,…(8分)
因为圆D过点O,F,且与直线x=4相切,
所以可设圆心D(
, m),半径为
,
于是圆D的方程为(x-
)2+(y-m)2=
,…(11分)
因为点O(0,0)在圆D上,
所以
+m2=
,解得m=2或m=-2,
所求圆的方程为(x-
)2+(y-2)2=
或(x-
)2+(y+2)2=
.…(14分)
 解:(1)因为△B1B2F为正三角形,OF=c,OB2=b,B2F=a,
解:(1)因为△B1B2F为正三角形,OF=c,OB2=b,B2F=a,所以e=
| c |
| a |
| OF |
| FB2 |
| ||
| 2 |
准线l的方程:x=
| a2 |
| c |
所以
|
|
于是b=
| 3 |
故椭圆方程为
| x2 |
| 12 |
| y2 |
| 3 |
(2)设所求圆的圆心为D,由(1)知椭圆的右准线方程为x=4,…(8分)
因为圆D过点O,F,且与直线x=4相切,
所以可设圆心D(
| 3 |
| 2 |
| 5 |
| 2 |
于是圆D的方程为(x-
| 3 |
| 2 |
| 25 |
| 4 |
因为点O(0,0)在圆D上,
所以
| 9 |
| 4 |
| 25 |
| 4 |
所求圆的方程为(x-
| 3 |
| 2 |
| 25 |
| 4 |
| 3 |
| 2 |
| 25 |
| 4 |
点评:本题考查椭圆的标准方程,涉及椭圆离心率的求解及直线与圆的位置关系,属中档题.

练习册系列答案
相关题目
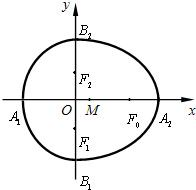 我们把由半椭圆
我们把由半椭圆 与半椭圆
与半椭圆 组成的曲线称为“果圆”,其中
组成的曲线称为“果圆”,其中 ,
, 是对应的焦点。A1,A2和B1,B2是“果圆”与x,y轴的交点,M是线段A1A2的中点.
是对应的焦点。A1,A2和B1,B2是“果圆”与x,y轴的交点,M是线段A1A2的中点. 是底边F1F2长为6,腰长为5的等腰三角形,求“果圆”的方程;
是底边F1F2长为6,腰长为5的等腰三角形,求“果圆”的方程; ,
, 过F0的直线l交“果圆”于y轴右边的Q,N点,求△OQN的面积S△OQN的取值范围
过F0的直线l交“果圆”于y轴右边的Q,N点,求△OQN的面积S△OQN的取值范围 是“果圆”上任意一点,求
是“果圆”上任意一点,求 取得最小值时点
取得最小值时点
 与半椭圆
与半椭圆 组成的曲线称为“果圆”,其中
组成的曲线称为“果圆”,其中 ,
, 是对应的焦点。A1,A2和B1,B2是“果圆”与x,y轴的交点,M是线段A1A2的中点.
是对应的焦点。A1,A2和B1,B2是“果圆”与x,y轴的交点,M是线段A1A2的中点. 是底边F1F2长为6,腰长为5的等腰三角形,求“果圆”的方程;
是底边F1F2长为6,腰长为5的等腰三角形,求“果圆”的方程; ,
, 过F0的直线l交“果圆”于y轴右边的Q,N点,求△OQN的面积S△OQN的取值范围
过F0的直线l交“果圆”于y轴右边的Q,N点,求△OQN的面积S△OQN的取值范围 是“果圆”上任意一点,求
是“果圆”上任意一点,求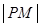 取得最小值时点
取得最小值时点