题目内容
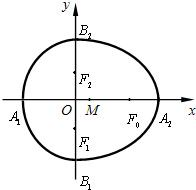 我们把由半椭圆
我们把由半椭圆| x2 |
| a2 |
| y2 |
| b2 |
| y2 |
| b2 |
| x2 |
| c2 |
(1)若△F0F1F2是边长为1的等边三角形,求该“果圆”的方程;
(2)设P是“果圆”的半椭圆
| y2 |
| b2 |
| x2 |
| c2 |
(3)若P是“果圆”上任意一点,求|PM|取得最小值时点P的横坐标.
分析:(1)根据焦点F0,F1,F2的坐标,分别求得|F0F2|和|F1F2|进而求得c2,则a可求得,进而求得果圆的方程.
(2)设P(x,y),则|PM|可求,根据1-
<0求得∴|PM|2的最小值只能在x=0或x=-c处取到.即|PM|取得最小值时,P在点B1,B2或A1处.原式得证.
(3)根据题意可知研究P位于“果圆”的半椭圆
+
=1 (x≥0)上的情形即可.先表示出|PM|进而根据x的范围确定a和c不等式关系,看a≤2c时,|PM|2的最小值在x=
时取到,根据|PM|2在x<a时是递减的进而可知|PM|2的最小值在x=a时取到,进而分别求得P的坐标.
(2)设P(x,y),则|PM|可求,根据1-
| b2 |
| c2 |
(3)根据题意可知研究P位于“果圆”的半椭圆
| x2 |
| a2 |
| y2 |
| b2 |
| a2(a-c) |
| 2c2 |
解答:解:(1)∵F0(c,0),F1(0,-
),F2(0,
),
∴|F0F2|=
=b=1,| F1F2|=2
=1,
于是c2=
,a2=b2+c2=
,
所求“果圆”方程为
x2+y2=1(x≥0),y2+
x2=1(x≤0).
(2)设P(x,y),则|PM|2=(x-
)2+y2=(1-
)x2-(a-c)x+
+b2,-c≤x≤0,
∵1-
<0,
∴|PM|2的最小值只能在x=0或x=-c处取到.
即当|PM|取得最小值时,P在点B1,B2或A1处.
(3)∵|A1M|=|MA2|,且B1和B2同时位于“果圆”的半椭圆
+
=1( x≥0 )和半椭圆
+
=1( x≤0 )上,
所以,由(2)知,只需研究P位于“果圆”的半椭圆
+
=1 (x≥0)上的情形即可.| PM|2=(x-
)2+y2=
[ x-
]2+b2+
-
.
当x=
≤a,即a≤2c时,|PM|2的最小值在x=
时取到,
此时P的横坐标是
.
当x=
>a,即a>2c时,
由于|PM|2在x<a时是递减的,|PM|2的最小值在x=a时取到,此时P的横坐标是a.
综上所述,若a≤2c,当|PM|取得最小值时,点P的横坐标是
;
若a>2c,当|PM|取得最小值时,点P的横坐标是a或-c.
| b2-c2 |
| b2-c2 |
∴|F0F2|=
| (b2-c2)+c2 |
| b2-c2 |
于是c2=
| 3 |
| 4 |
| 7 |
| 4 |
所求“果圆”方程为
| 4 |
| 7 |
| 4 |
| 3 |
(2)设P(x,y),则|PM|2=(x-
| a-c |
| 2 |
| b2 |
| c2 |
| (a-c)2 |
| 4 |
∵1-
| b2 |
| c2 |
∴|PM|2的最小值只能在x=0或x=-c处取到.
即当|PM|取得最小值时,P在点B1,B2或A1处.
(3)∵|A1M|=|MA2|,且B1和B2同时位于“果圆”的半椭圆
| x2 |
| a2 |
| y2 |
| b2 |
| y2 |
| b2 |
| x2 |
| c2 |
所以,由(2)知,只需研究P位于“果圆”的半椭圆
| x2 |
| a2 |
| y2 |
| b2 |
| a-c |
| 2 |
| c2 |
| a2 |
| a2(a-c) |
| 2c2 |
| (a-c)2 |
| 4 |
| a2(a-c)2 |
| 4c2 |
当x=
| a2(a-c) |
| 2c2 |
| a2(a-c) |
| 2c2 |
此时P的横坐标是
| a2(a-c) |
| 2c2 |
当x=
| a2(a-c) |
| 2c2 |
由于|PM|2在x<a时是递减的,|PM|2的最小值在x=a时取到,此时P的横坐标是a.
综上所述,若a≤2c,当|PM|取得最小值时,点P的横坐标是
| a2(a-c) |
| 2c2 |
若a>2c,当|PM|取得最小值时,点P的横坐标是a或-c.
点评:本题主要考查了椭圆的应用.考查了学生综合分析问题和基本的运算能力.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
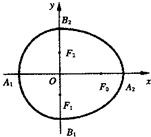 我们把由半椭圆
我们把由半椭圆 我们把由半椭圆
我们把由半椭圆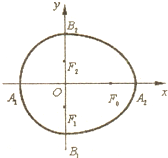 请阅读以下材料,然后解决问题:
请阅读以下材料,然后解决问题: