题目内容
(本题满分12分)在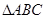 中,
中,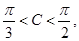 且
且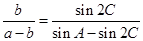 .
.
(1)判断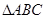 的形状;
的形状;
(2)若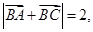 求
求 的取值范围.
的取值范围.
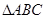 中,
中,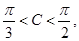 且
且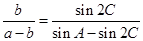 .
.(1)判断
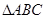 的形状;
的形状;(2)若
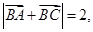 求
求 的取值范围.
的取值范围.(1)三角形为等腰三角形.(2)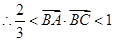 .
.
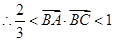 .
.(1)由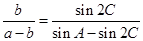 得
得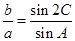 ,再根据正弦定理
,再根据正弦定理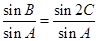 .
.
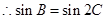 ,所以
,所以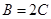 或
或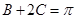 ,然后再根据C的范围,及三角形内角和定理求出A,B,C的值.
,然后再根据C的范围,及三角形内角和定理求出A,B,C的值.
(II)若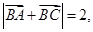 则边
则边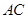 上的中线长1.
上的中线长1.
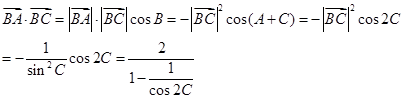
从而得到关于C的函数关系式,转化为函数值域问题来解决.
(1)由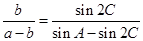 可得
可得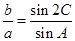 ,
,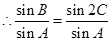 ,
,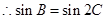
所以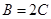 或
或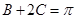 ,
,
因为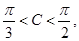 若
若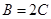 ,则
,则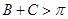 .
.
所以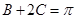 ,由
,由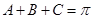 ,相减得:
,相减得: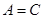
三角形为等腰三角形.
(2)若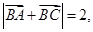 则边
则边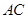 上的中线长1.
上的中线长1.
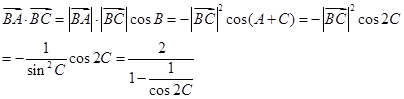

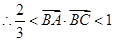 .
.
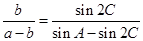 得
得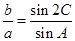 ,再根据正弦定理
,再根据正弦定理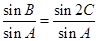 .
.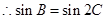 ,所以
,所以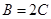 或
或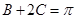 ,然后再根据C的范围,及三角形内角和定理求出A,B,C的值.
,然后再根据C的范围,及三角形内角和定理求出A,B,C的值.(II)若
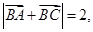 则边
则边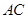 上的中线长1.
上的中线长1.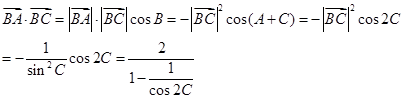
从而得到关于C的函数关系式,转化为函数值域问题来解决.
(1)由
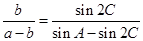 可得
可得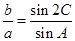 ,
,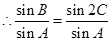 ,
,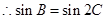
所以
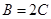 或
或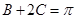 ,
,因为
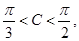 若
若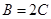 ,则
,则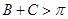 .
.所以
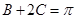 ,由
,由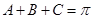 ,相减得:
,相减得: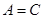
三角形为等腰三角形.
(2)若
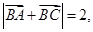 则边
则边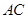 上的中线长1.
上的中线长1.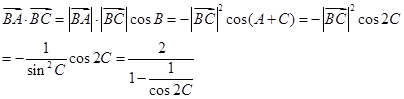

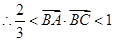 .
.
练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 ,则
,则 等于( )
等于( )



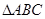 中,
中,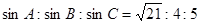 ,则角A =
,则角A = 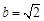 ,c=1,
,c=1, ,求A ,C, a.
,求A ,C, a. 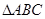 中,已知
中,已知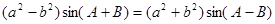 ,判定
,判定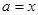 ,
, ,若ΔABC有两解,则
,若ΔABC有两解,则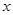 的取值范围是( )
的取值范围是( )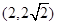
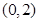
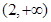
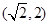
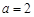 ,
, ,
, .
. .
.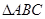 中,若
中,若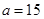 ,
,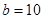 ,
,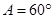 ,则
,则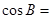 ( )
( )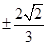
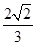
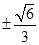
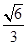
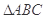 中,
中,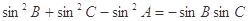 ,则A= ( )
,则A= ( )