题目内容
(1)利用函数单调性的定义证明函数h(x)=x+
在[
,∞)上是增函数;
(2)我们可将问题(1)的情况推广到以下一般性的正确结论:已知函数y=x+
有如下性质:如果常数t>0,那么该函数在(0,
]上是减函数,在[
,+∞)上是增函数.
若已知函数f(x)=
,x∈[0,1],利用上述性质求出函数f(x)的单调区间;又已知函数g(x)=-x-2a,问是否存在这样的实数a,使得对于任意的x1∈[0,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,若不存在,请说明理由;如存在,请求出这样的实数a的值.
| 3 |
| x |
| 3 |
(2)我们可将问题(1)的情况推广到以下一般性的正确结论:已知函数y=x+
| t |
| x |
| t |
| t |
若已知函数f(x)=
| 4x2-12x-3 |
| 2x+1 |
分析:(1)利用函数单调性的定义进行证明.
(2)根据推广的结论,确定函数f(x)的单调区间,利用条件g(x2)=f(x1)成立,建立条件关系,即可求a.
(2)根据推广的结论,确定函数f(x)的单调区间,利用条件g(x2)=f(x1)成立,建立条件关系,即可求a.
解答:解:(1)设x1,x2∈[
,+∞),且x1<x2,
则f(x1)-f(x2)=x1+
-x2-
=
,
∵x2>x1≥
,∴x1-x2>0,x1x2>3.
∴f(x1)-f(x2)<0,
即f(x1)<f(x2),
因此,函数在给定的区间上单调递增.
(2)∵y=f(x)=
=2x+1+
-8,
设u=2x+1,x∈[0,1],
则1≤u≤3,
则y=u+
-8,u∈[1,3],
由已知性质得,
当1≤u≤2,即0≤x≤
时,f(x)单调递减,
∴递减区间为[0,
],
当2≤u≤3,即
≤x≤1时,f(x)单调递增,
∴递增区间为[
,1].
由f(0)=-3,f(
)=-4,f(1)=-
,
得f(x)的值域为[-4,-3],
由于g(x)=-x-2a为减函数,
故g(x)∈[-1-2a,-2a],x∈[0,1]
由题意,f(x)的值域为g(x)的值域的子集,
从而有
,
∴a=
,
∴存在满足条件的值.
| 3 |
则f(x1)-f(x2)=x1+
| 3 |
| x1 |
| 3 |
| x2 |
| (x1-x2)(x1x2-3) |
| x1x2 |
∵x2>x1≥
| 3 |
∴f(x1)-f(x2)<0,
即f(x1)<f(x2),
因此,函数在给定的区间上单调递增.
(2)∵y=f(x)=
| 4x2-12x-3 |
| 2x+1 |
| 4 |
| 2x+1 |
设u=2x+1,x∈[0,1],
则1≤u≤3,
则y=u+
| 4 |
| u |
由已知性质得,
当1≤u≤2,即0≤x≤
| 1 |
| 2 |
∴递减区间为[0,
| 1 |
| 2 |
当2≤u≤3,即
| 1 |
| 2 |
∴递增区间为[
| 1 |
| 2 |
由f(0)=-3,f(
| 1 |
| 2 |
| 11 |
| 3 |
得f(x)的值域为[-4,-3],
由于g(x)=-x-2a为减函数,
故g(x)∈[-1-2a,-2a],x∈[0,1]
由题意,f(x)的值域为g(x)的值域的子集,
从而有
|
∴a=
| 3 |
| 2 |
∴存在满足条件的值.
点评:本题主要考查函数单调性的判断和证明,以及对勾函数的性质,考查学生的理解和应用能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 在
在 上的单调性;
上的单调性; ,求函数
,求函数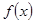 在
在 。
。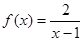 ,
,