题目内容
当不等式组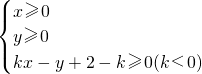 所表示的平面区域的面积最小时,实数k的值为
所表示的平面区域的面积最小时,实数k的值为
- A.-

- B.-

- C.-1
- D.-2
B
分析:由于不等式组所表示的平面区域由三条直线围成,其中直线kx-y+2-k=0(k<0)即y-2=k(x-1)(k<0)经过定点(1,2),
因此问题转化为求经过定点(1,2)的直线与两坐标轴在第一象限内所围成的三角形的面积的最小值.
解答:由于不等式组所表示的平面区域由三条直线围成,其中直线kx-y+2-k=0(k<0)即y-2=k(x-1)(k<0)经过定点(1,2),
因此问题转化为求经过定点(1,2)的直线与两坐标轴在第一象限内所围成的三角形的面积的最小值.
如图所示,设所围成的区域的面积为S,则S= •|OA|•|OB|=
•|OA|•|OB|= •|2-k|•|1-
•|2-k|•|1- |.
|.
因为k<0,
所以-k>0,
所以S= (4-k-
(4-k-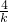 )=
)= [4+(-k)+(-
[4+(-k)+(-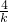 )]≥
)]≥ [4+2
[4+2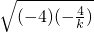 ]=4,
]=4,
当S取得最小值4时,-k=-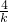 ,解得k=-2.
,解得k=-2.
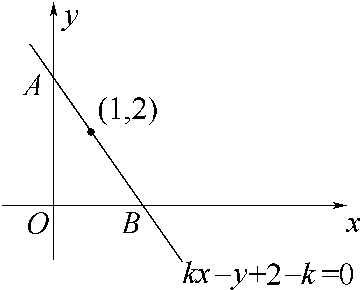
故选D
点评:此题考查了不等式组表示平面区域,还考查了直线的方程及三角形的面积公式和均值不等式求函数的最值.
分析:由于不等式组所表示的平面区域由三条直线围成,其中直线kx-y+2-k=0(k<0)即y-2=k(x-1)(k<0)经过定点(1,2),
因此问题转化为求经过定点(1,2)的直线与两坐标轴在第一象限内所围成的三角形的面积的最小值.
解答:由于不等式组所表示的平面区域由三条直线围成,其中直线kx-y+2-k=0(k<0)即y-2=k(x-1)(k<0)经过定点(1,2),
因此问题转化为求经过定点(1,2)的直线与两坐标轴在第一象限内所围成的三角形的面积的最小值.
如图所示,设所围成的区域的面积为S,则S=
 •|OA|•|OB|=
•|OA|•|OB|= •|2-k|•|1-
•|2-k|•|1- |.
|.因为k<0,
所以-k>0,
所以S=
 (4-k-
(4-k-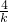 )=
)= [4+(-k)+(-
[4+(-k)+(-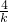 )]≥
)]≥ [4+2
[4+2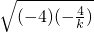 ]=4,
]=4,当S取得最小值4时,-k=-
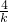 ,解得k=-2.
,解得k=-2.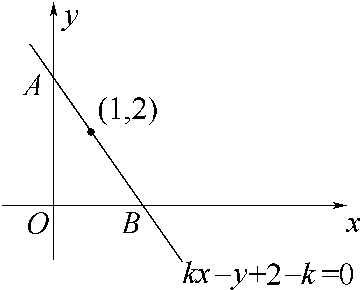
故选D
点评:此题考查了不等式组表示平面区域,还考查了直线的方程及三角形的面积公式和均值不等式求函数的最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
当不等式组
所表示的平面区域的面积最小时,实数k的值为( )
|
A、-
| ||
B、-
| ||
| C、-1 | ||
| D、-2 |
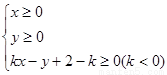 所表示的平面区域的面积最小时,实数k的值为( )
所表示的平面区域的面积最小时,实数k的值为( ) 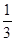 B.-
B.-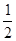 C.-1 D.-2
C.-1 D.-2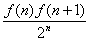 所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)的个数为f(n)(n∈N*).
所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)的个数为f(n)(n∈N*).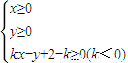 所表示的平面区域的面积最小时,实数k的值为( )
所表示的平面区域的面积最小时,实数k的值为( )
