Question

设不等式组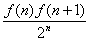所表示的平面区域为D_n,记D_n内的格点(格点即横坐标和纵坐标均为整数的点)的个数为f(n)(n∈N^*).

(1)求f(1),f(2)的值及f(n)的表达式.(可以不作证明)

(2)记T_n=,若对于一切正整数n,总有T_n≤m成立,求实数m的取值范围.

(3)求证:当n∈N^*时,++…+＜.

Answer 1

解:(1)f(1)=3,f(2)=6.直线y=-nx+3n恒过点(3,0)且斜率k=-n＜0,

∴x只能取1,2.当x=1时,y=2n,可取格点2n个;当x=2时,y=n,可取格点n个.

∴f(n)=3n.(2)T_n==,

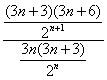∵==,当n=1时,＞1;当n=2时,=1;当n≥3时,＜1.

∴T₁＜T₂=T₃＞T₄＞…＞T_n.故T_n的最大值是T₂=T₃=,∴m≥.

(3)由(1)可知++…+=(++…+),

∵(++…+)²＜()［()²+()²+…+()²］

＜n［++…+］

=n(++…)=.

∴++…+＜,得证.