题目内容
过△ABC的重心G任作一条直线EF，AD⊥EF于D，BE⊥EF于E，CF⊥EF于F，则向量
，
，
之间正确的关系是（ ）
| AD |
| BE |
| CF |
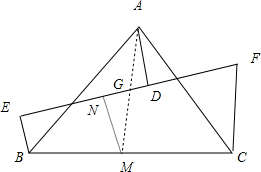
分析：设BC边的中点为M，过M做MN⊥EF，由三角形的重心的性质可得
=2
，则可得
=2
，再由M为BC的中点可得
=
(
+
)，从而可求
| AG |
| GM |
| AD |
| NM |
| MN |
| 1 |
| 2 |
| BE |
| CF |
解答：解：设BC边的中点为M，过M做MN⊥EF，
由三角形的重心的性质可得，AG=2GM，即
=2
∴
=2
①
∵BE，MN，CF都与EF垂直
∴BE∥MN∥CF
∵M为BC的中点
=
(
+
)②
由①②可得，
=-(
+
)
∴
+
+
=
故选：D
由三角形的重心的性质可得，AG=2GM，即
| AG |
| GM |
∴
| AD |
| NM |
∵BE，MN，CF都与EF垂直
∴BE∥MN∥CF
∵M为BC的中点
| MN |
| 1 |
| 2 |
| BE |
| CF |
由①②可得，
| AD |
| BE |
| CF |
∴
| AD |
| BE |
| CF |
| 0 |
故选：D
点评：本题主要考查了向量的基本关系在三角形中的应用，解题的关键是根据三角形的重心的性质得到AD与MN的长度关系．
练习册系列答案
备战中考寒假系列答案
相关题目
，
，
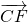之间正确的关系是
，
，
之间正确的关系是（ ）
+3
+3
=0
+2
+2
=0
+2
+
=0
+
+
=0