Question

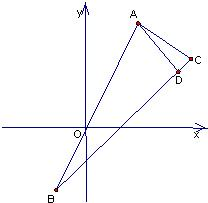已知在△ABC中，A（2，4），B（-1，-2），C（4，3），BC边上的高为AD，垂足为D：
（1）求证：AB⊥AC；
（2）求点D和向量

AD

的坐标；
（3）设∠ABC=θ，求cosθ的值；
（4）求证：AD²=BD•DC．

Answer 1

分析：（1）写出向量

BA

和

AC

的坐标，只要证明数量积为0即可．
（2）由D在BC上，所以存在实数λ使

BD

=λ

BC

，可由λ表达出D的坐标，再由AD⊥BC可求出λ，继而可求得点D和向量

AD

的坐标．
（3）直接由夹角公式求解即可．
（4）由两点间的距离公式分别求等式两边的距离即可．

解答：解：（1）

BA

=（3，6），

AC

=（2，-1），所以

BA

•

AC

=3×2+6×（-1）=0，
所以AB⊥AC
（2）由D在BC上，所以存在实数λ使

BD

=λ

BC

=（5λ，5λ），所以D（5λ-1，5λ-2）
所以

AD

=（5λ-3，5λ-6），由AD⊥BC得

AD

•

BC

=（5λ-3，5λ-6）（5，5）=0，λ=

9

10

所以D（

7

2

，

5

2

），

AD

=（

3

2

，-

3

2

）
（3）cosθ=

BA • BC

| BA || BC |

=

45

9+36 25+25

=

3 10

10

（4）

AD

2=

9

4

+

9

4

=

9

2

BD=

( 7 2 +1)2+ ( 5 2 +2)2

=

9 2

2

，DC=

(4- 7 2 )2+(3- 5 2 )2

=

2

2

所以BD•DC=

9

2

=AD²

点评：本题考查点的坐标和向量的坐标、向量的夹角公式、两个向量共线和垂直的条件等知识，考查运算能力．