题目内容
【题目】已知函数f(x)=lnx+ax在点(t,f(t))处的切线方程为y=3x+1
(1)求a的值;
(2)已知k≤2,当x>1时,f(x)>k(1﹣ ![]() )+2x﹣1恒成立,求实数k的取值范围;
)+2x﹣1恒成立,求实数k的取值范围;
(3)对于在(0,1)中的任意一个常数b,是否存在正数x0 , 使得e ![]() +
+ ![]() x02<1?请说明理由.
x02<1?请说明理由.
【答案】
(1)解:函数f(x)=lnx+ax的导数为f′(x)= ![]() +a,
+a,
在点(t,f(t))处切线方程为y=3x+1,
可得f′(t)= ![]() +a,
+a,
∴函数的切线方程为y﹣(lnt+at)=( ![]() +a)(x﹣t),即y=(
+a)(x﹣t),即y=( ![]() +a)x+lnt﹣1,
+a)x+lnt﹣1,
∴ 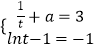 ,
,
解得a=2;
(2)证明:由(1)可得f(x)=lnx+2x,
∵f(x)>k(1﹣ ![]() )+2x﹣1,
)+2x﹣1,
∴lnx>k(1﹣ ![]() )﹣1
)﹣1
即为xlnx+x﹣k(x﹣3)>0,
可令g(x)=xlnx+x﹣k(x﹣3),
g′(x)=2+lnx﹣k,
由x>1,可得lnx>0,2﹣k≥0,
即有g′(x)>0,g(x)在(1,+∞)递增,
可得g(x)>g(1)=1+2k≥0,
∴﹣ ![]() ≤k≤2
≤k≤2
故k的取值范围为[﹣ ![]() ,2];
,2];
(3)解:对于在(0,1)中的任意一个常数b,
假设存在正数x0,使得:e ![]() +
+ ![]() x02<1.
x02<1.
由ef(x0+1)﹣3x0﹣2+ ![]() x02=eln(x0+1)﹣x0+
x02=eln(x0+1)﹣x0+ ![]() x02=(x0+1)e﹣x0+
x02=(x0+1)e﹣x0+ ![]() x02<1成立,
x02<1成立,
从而存在正数x0,使得上式成立,只需上式的最小值小于0即可.
令H(x)=(x+1)e﹣x+ ![]() x2﹣1,H′(x)=e﹣x﹣(x+1)e﹣x+bx=x(b﹣e﹣x),
x2﹣1,H′(x)=e﹣x﹣(x+1)e﹣x+bx=x(b﹣e﹣x),
令H′(x)>0,解得x>﹣lnb,令H′(x)<0,解得0<x<﹣lnb,
则x=﹣lnb为函数H(x)的极小值点,即为最小值点.
故H(x)的最小值为H(﹣lnb)=(﹣lnb+1)elnb+ ![]() ln2b﹣1=
ln2b﹣1= ![]() ln2b﹣blnb+b﹣1,
ln2b﹣blnb+b﹣1,
再令G(x)= ![]() ln2x﹣xlnx+x﹣1,(0<x<1),
ln2x﹣xlnx+x﹣1,(0<x<1),
G′(x)= ![]() (ln2x+2lnx)﹣(1+lnx)+1=ln2x>0,
(ln2x+2lnx)﹣(1+lnx)+1=ln2x>0,
则G(x)在(0,1)递增,可得G(x)<G(1)=0,则H(﹣lnb)<0.
故存在正数x0=﹣lnb,使得e ![]() +
+![]() x02<1.
x02<1.
【解析】(1)求出f(x)的导数,可得切线的斜率和切点,解方程可得a的值;(2)求出f(x)=lnx+x,要证原不等式成立,即证xlnx+x﹣k(x﹣3)>0,可令g(x)=xlnx+x﹣k(x﹣3),求出导数,判断符号,可得单调性,即可得证;(3)对于在(0,1)中的任意一个常数b,假设存在正数x0 , 使得e ![]() +
+ ![]() x02<1.运用转化思想可令H(x)=(x+1)e﹣x+
x02<1.运用转化思想可令H(x)=(x+1)e﹣x+ ![]() x2﹣1,求出导数判断单调性,可得最小值,即可得到结论
x2﹣1,求出导数判断单调性,可得最小值,即可得到结论

【题目】自2017年2月底,90多所自主招生试点高校将陆续出台2017年自主招生简章,某校高三年级选取了在期中考试中成绩优异的100名学生作为调查对象,对是否准备参加2017年的自主招生考试进行了问卷调查,其中“准备参加”“不准备参加”和“待定”的人数如表:
准备参加 | 不准备参加 | 待定 | |
男生 | 30 | 6 | 15 |
女生 | 15 | 9 | 25 |
(1)在所有参加调查的同学中,在三种类型中用分层抽样的方法抽取20人进行座谈交流,则在“准备参加”“不准备参加”和“待定”的同学中应各抽取多少人?
(2)在“准备参加”的同学中用分层抽样方法抽取6人,从这6人中任意抽取2人,求至少有一名女生的概率.

