Question

【题目】空间几何体ABCDEF如图所示．已知面ABCD⊥面ADEF，ABCD为梯形，ADEF为正方形，且AB∥CD，AB⊥AD，CD=4，AB=AD=2，G为CE的中点． （Ⅰ）求证：BG∥面ADEF；
（Ⅱ）求证：面DBG⊥面BDF．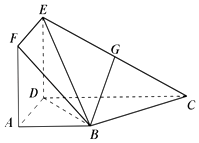

Answer 1

【答案】证明：（ I）如图1，取ED中点H，连接HG、AH， 因为G、H分别为EC、ED的中点，所以HG∥CD且
因为AB∥CD且
所以AB∥HG，且AB=HG．
所以AHGB为平行四边形，所以AH∥BG；
因为BG面PBC，AH面PBC，所以BG∥面ADEF；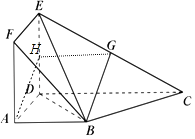

图1
（Ⅱ）如图2，∵ABCD⊥面ADEF及ED⊥DCED⊥面ADCDED⊥DC．
取BD中点O，连接OF，OG、DG
∵AB⊥AD，CD=4，AB=AD=2，∴BF=DF=DB=2 ，OF⊥BD，OF= ，
∵BG=AH= ，DG= EC= ，∴OG⊥BD，OG=
∴∠FOG为二面角F﹣BD﹣G的平面角；
在△OFG中，OF= ，OG= ，FG= ，
满足OF2+OG2=FG2 ， ∴∠FOG为直角，
∴面DBG⊥面BDF．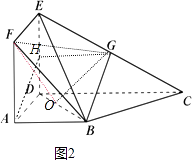

【解析】（Ⅰ）取ED中点H，连接HG、AH，只需证明AH∥BG即可；（Ⅱ）取BD中点O，连接OF，OG、DG，易得∠FOG为二面角F﹣BD﹣G的平面角，解△OFG即可．
【考点精析】通过灵活运用直线与平面平行的判定和平面与平面垂直的判定，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行；一个平面过另一个平面的垂线，则这两个平面垂直即可以解答此题．