题目内容
在△ABC中,若 ,则其面积等于( )
,则其面积等于( )
A. | B. | C. | D. |
D
解析试题分析:已知三条边长利用余弦定理求得cosC=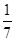 再利用同角三角函数的基本关系求得
再利用同角三角函数的基本关系求得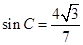 ,代入△ABC的面积公式进行运算.解:△ABC中,若三边长分别为a=7,b=3,c=8,由余弦定理可得64="49+9-2×7×3" cosC,解得cosC=
,代入△ABC的面积公式进行运算.解:△ABC中,若三边长分别为a=7,b=3,c=8,由余弦定理可得64="49+9-2×7×3" cosC,解得cosC=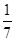 ,则可知
,则可知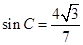 ,因此其面积公式为
,因此其面积公式为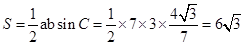 ,故选D.
,故选D.
考点:余弦定理
点评:本题考查余弦定理的应用,同角三角函数的基本关系,求出sinC的值是解题的关键。

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
在 中,已知
中,已知 ,则这个三角形解的情况是( )
,则这个三角形解的情况是( )
| A.有一个解 | B.有两个解 | C.无解 | D.不能确定 |
若△ABC能被一条直线分成两个与自身相似的三角形,那么这个三角形的形状是( )
| A.钝角三角形 | B.直角三角形 |
| C.锐角三角形 | D.不能确定 |
已知 ,则
,则 =( )
=( )
| A.4 | B.5 | C.6 | D.7 |
在 中,角
中,角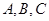 所对的边分
所对的边分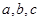 .若
.若 ,则
,则 ( )
( )
A.-  | B. | C.-1 | D.1 |
△ABC中,已知 60°,如果△ABC 两组解,则x的取值范围( )
60°,如果△ABC 两组解,则x的取值范围( )
A. | B. | C. | D. |
三角形两条边长分别为2和3,其夹角的余弦值是方程2 -3x+1=0的根,则此三角形周长为
-3x+1=0的根,则此三角形周长为
A. | B.7 | C.5+ | D.5+2 |
如图,在地面 处测得树梢的仰角为60°,
处测得树梢的仰角为60°, 与树底部
与树底部 相距为5米,则树高为( )
相距为5米,则树高为( )
A. 米 米 | B.5米 | C.10米 | D. 米 米 |
已知 中,
中,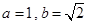 ,
, ,则角
,则角 等于( )
等于( )
A. | B. | C. | D. |