题目内容
已知函数![]()
![]() ,函数
,函数![]() 的图像与函数
的图像与函数![]()
![]() 的图像关于直线
的图像关于直线![]() 对称.
对称.
(1)求函数![]() 的解析式;
的解析式;
(2)若函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,
,
求实数![]() 的取值范围;
的取值范围;
(3)设函数![]()
![]() ,试用列举法表示集合
,试用列举法表示集合![]() .
.
(1) (2)
(2) ![]()
(3)![]()
解析:
(1)由![]() 得
得![]() ,由已知可得
,由已知可得
 (4分)
(4分)
(2)![]() 在
在![]() 上是单调递增的,又
上是单调递增的,又![]() ,
,
(或设![]()
![]() 则
则![]()
![]()
![]() ,
,
![]() )
)
所以函数![]() 在区间
在区间![]() 上为增函数,因此 (6分)
上为增函数,因此 (6分)
![]()
即![]()
所以 m、n是方程![]() 的两个相异的解. (8分)
的两个相异的解. (8分)
设![]() ,则
,则 (10分)
(10分)
所以![]() 为所求. (12分)
为所求. (12分)
另解:由![]() 可转化为函数
可转化为函数![]() 图像与函数
图像与函数![]() 的图像有两个交点问题,数形结合求得:
的图像有两个交点问题,数形结合求得:![]() .
.
(3)![]() (14分)
(14分)
![]()
![]() 当且仅当
当且仅当![]() 时等号成立,
时等号成立,
 (16分)
(16分)
![]() ,
,![]() 有可能取的整数有且只有1,2,3.
有可能取的整数有且只有1,2,3.
当![]() 时,解得
时,解得![]() (舍去);
(舍去);
当![]() 时,解得
时,解得![]() (舍去);
(舍去);
当![]() 时,解得
时,解得![]() (舍去).故集合
(舍去).故集合![]() (18分)
(18分)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 和函数
和函数 的图像关于直线
的图像关于直线 对称,
对称, ,其中
,其中 ,则下列结论中正确的是( )
,则下列结论中正确的是( ) 的最大值为2
的最大值为2  的图像向左平移
的图像向左平移 得到函数
得到函数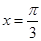
 。
。 的图象经过怎样的变换得到?
的图象经过怎样的变换得到? ,最大值为
,最大值为 。
。 的单调区间与函数
的单调区间与函数 的单调区间相同。故当
的单调区间相同。故当 ,解得x的范围即为所求的区间。
,解得x的范围即为所求的区间。 个单位长度,再把横坐标缩短为原来的
个单位长度,再把横坐标缩短为原来的 (纵坐标不变),然后把纵坐标伸长为原来的
(纵坐标不变),然后把纵坐标伸长为原来的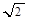 倍(横坐标不变),再向上平移1个单位即可。
倍(横坐标不变),再向上平移1个单位即可。 的最小正周期为
的最小正周期为
 所求的增区间为
所求的增区间为 ,
,
 即
即
 ,
, 。
。