题目内容
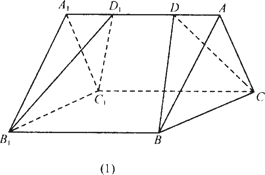
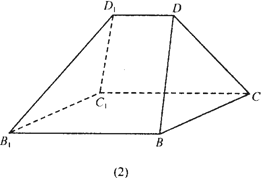
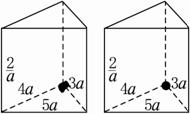
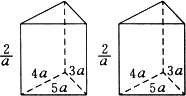
如图，有两个相同的直三棱柱，高为
，底面三角形的三边长分别为3a、4a、5a(a＞0)．用它们拼成一个三棱柱或四棱柱，在所有可能的情形中，全面积最小的是一个四棱柱，则a的取值范围是________．
答案：
解析：
提示：
解析：
|
答案： 解析：底面积为6a2，侧面面积分别为6、8、10，拼成三棱柱时，有三种情况： S1＝2×6a2＋2(10＋8＋6)＝12a2＋48， S2＝24a2＋2(10＋8)＝24a2＋36， S3＝24a2＋2(10＋6)＝24a2＋32． 拼成四棱柱时有一种： 全面积为(8＋6)×2＋4×6a2＝24a2＋28． 由题意得24a2＋28＜12a2＋48， |
提示：
|
有关多面体的拼接问题要注意考虑各种可能的情况，当为四棱柱时，全面积最小，需把两侧面面积最大的接合． |
练习册系列答案
阅读快车系列答案
相关题目
与房屋长度
等长，有两个坡面需铺上瓦片．
比房屋长度
，宽BC=2b，屋脊高为h，试问哪种方案尖顶铺设的瓦片比较省？说明理由．
，底面三角形的三边长分别为