题目内容
学习合情推理后,甲、乙两位同学各举了一个例子,甲:由“若三角形周长为l,面积为S,则其内切圆半径r=
”类比可得“若三棱锥表面积为S,体积为V,则其内切球半径r=
”;乙:由“若直角三角形两直角边长分别为a,b,则其外接圆半径r=
”;类比可得“若三棱锥三条侧棱两两垂直,侧棱长分别为a、b、c,则其外接球半径r=
”.这两位同学类比得出的结论( )
| 2S |
| l |
| 3V |
| S |
| ||
| 2 |
| ||
| 3 |
| A、两人都对 | B、甲错、乙对 |
| C、甲对、乙错 | D、两人都错 |
分析:本题考查的知识点是类比推理,但归纳推理和类比推理的结论不一定正确,我们还要继续进一步证明结论,由此三棱锥的外接球半径等于长方体的外接球半径,可求得其半径r=
,因此,乙同学类比的结论是错误的.
| ||
| 2 |
解答:解:利用等面积与等体积法可推得甲同学类比的结论是正确的;
把三条侧棱两两垂直的三棱锥补成一个长方体,
则此三棱锥的外接球半径等于长方体的外接球半径,
可求得其半径r=
,
因此,乙同学类比的结论是错误的.
故选C
把三条侧棱两两垂直的三棱锥补成一个长方体,
则此三棱锥的外接球半径等于长方体的外接球半径,
可求得其半径r=
| ||
| 2 |
因此,乙同学类比的结论是错误的.
故选C
点评:类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).判断一个推理过程是否是类比推理关键是看他是否符合类比推理的定义,即是否是由特殊到与它类似的另一个特殊的推理过程.

练习册系列答案
相关题目
 ,面积为S,则其内切圆半径
,面积为S,则其内切圆半径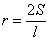 ”类比可得“若三棱锥表面积为S,体积为V,则其内切球半径
”类比可得“若三棱锥表面积为S,体积为V,则其内切球半径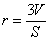 ”;乙:由“若直角三角形两直角边长分别为
”;乙:由“若直角三角形两直角边长分别为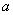 ,b,则其外接圆半径
,b,则其外接圆半径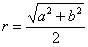 ”;类比可得“若三棱锥三条侧棱两两垂直,侧棱长分别为
”;类比可得“若三棱锥三条侧棱两两垂直,侧棱长分别为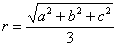 ”.这两位同学类比得出的结论 ( )
”.这两位同学类比得出的结论 ( )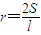 ”类比可得“若三棱锥表面积为S,体积为V,则其内切球半径
”类比可得“若三棱锥表面积为S,体积为V,则其内切球半径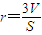 ”;乙:由“若直角三角形两直角边长分别为a,b,则其外接圆半径
”;乙:由“若直角三角形两直角边长分别为a,b,则其外接圆半径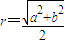 ”;类比可得“若三棱锥三条侧棱两两垂直,侧棱长分别为a、b、c,则其外接球半径
”;类比可得“若三棱锥三条侧棱两两垂直,侧棱长分别为a、b、c,则其外接球半径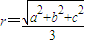 ”.这两位同学类比得出的结论( )
”.这两位同学类比得出的结论( )