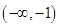题目内容
(本小题满分12分)设定义域都为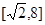 的两个函数
的两个函数 的解析式分别为
的解析式分别为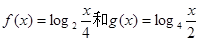
 ,
,
(1)求函数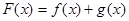 的值域;
的值域;
(2)求函数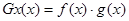 的值域.
的值域.
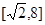 的两个函数
的两个函数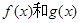 的解析式分别为
的解析式分别为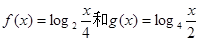
 ,
,(1)求函数
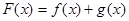 的值域;
的值域;(2)求函数
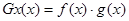 的值域.
的值域.(1)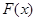 的值域为
的值域为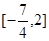 。(2)
。(2)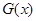 的值域为
的值域为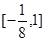
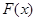 的值域为
的值域为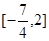 。(2)
。(2) 的值域为
的值域为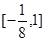
本试题主要是考查了对数函数的性质和二次函数的最值的运用。
(1)由已知及对数的运算性质可得,

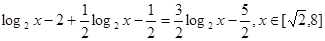 ,结合对数函数的性质得到最值。
,结合对数函数的性质得到最值。
(2)由已知及对数的运算性质可得,
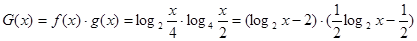
=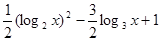 ,
,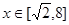 ,然后结合二次函数性质得到最值。
,然后结合二次函数性质得到最值。
(1)由已知及对数的运算性质可得,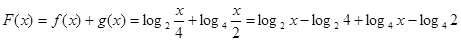
= ,-----2分
,-----2分
因为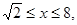 且
且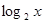 的值随着x的增大而增大,----------3分
的值随着x的增大而增大,----------3分
所以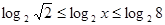 ,即
,即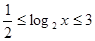 ,--------4分
,--------4分
故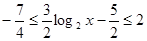 ,即
,即 ---------------5分
---------------5分
所以函数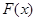 的值域为
的值域为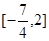 ---------------------6分
---------------------6分
(2)由已知及对数的运算性质可得,
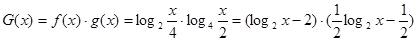
=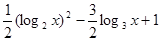 ,
,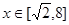 ,--------8分
,--------8分
令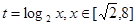 ,则有
,则有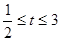 ,
,
于是有函数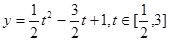 ,
,
所以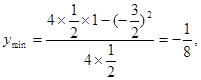
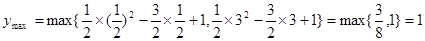 --------11分
--------11分
因此 ,即
,即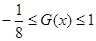 ,
,
所以函数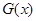 的值域为
的值域为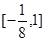 .-----------12分
.-----------12分
(1)由已知及对数的运算性质可得,

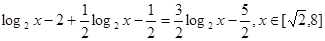 ,结合对数函数的性质得到最值。
,结合对数函数的性质得到最值。(2)由已知及对数的运算性质可得,
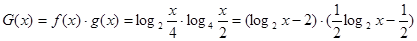
=
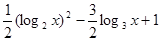 ,
,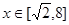 ,然后结合二次函数性质得到最值。
,然后结合二次函数性质得到最值。(1)由已知及对数的运算性质可得,
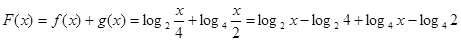
=
 ,-----2分
,-----2分因为
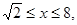 且
且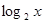 的值随着x的增大而增大,----------3分
的值随着x的增大而增大,----------3分所以
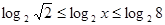 ,即
,即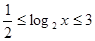 ,--------4分
,--------4分故
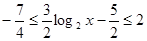 ,即
,即 ---------------5分
---------------5分所以函数
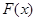 的值域为
的值域为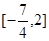 ---------------------6分
---------------------6分(2)由已知及对数的运算性质可得,
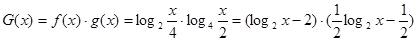
=
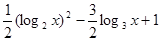 ,
,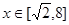 ,--------8分
,--------8分令
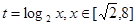 ,则有
,则有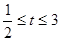 ,
,于是有函数
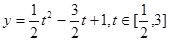 ,
,所以
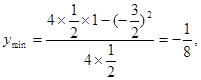
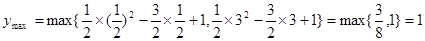 --------11分
--------11分因此
 ,即
,即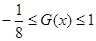 ,
,所以函数
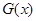 的值域为
的值域为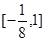 .-----------12分
.-----------12分
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
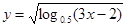 的定义域是_______
的定义域是_______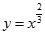 ,则其值域为
,则其值域为 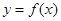 定义域为
定义域为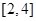 ,则
,则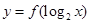 的定义域为( )
的定义域为( )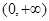
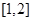
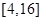
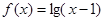 的定义域是
的定义域是 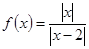 为偶函数; (2)函数
为偶函数; (2)函数 ;
;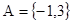 ,
,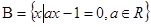 ,若
,若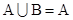 ,则实数
,则实数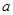 的取值集合为
的取值集合为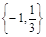 ; (4)集合
; (4)集合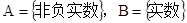 ,对应法则f:“求平方根”,则
,对应法则f:“求平方根”,则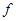 是A到B的映射;你认为正确命题的序号是 (把正确的序号都写上).
是A到B的映射;你认为正确命题的序号是 (把正确的序号都写上).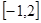 ,求f(2x+1)的定义域.(8分)
,求f(2x+1)的定义域.(8分) 的定义域为( )
的定义域为( )



 的定义域是
的定义域是