题目内容
用一块长为a,宽为b(a>b)的矩形木板,在二面角为α的墙角处围出一个直三棱柱的谷仓,试问应怎样围才能使谷仓的容积最大?并求出谷仓容积的最大值.
当木板的长边着地,并且谷仓的底面是以a为底边的等腰三角形时,谷仓的容积最大,其最大值为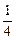 a2bcos
a2bcos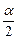 .
.
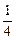 a2bcos
a2bcos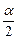 .
. 如图,设矩形木板的长边AB着地,并设OA=x,OB=y,则a2=x2+y2-2xycosα≥2xy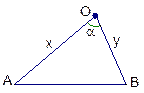
-2xycosα=2xy(1-cosα).
∵0<α<π,∴1-cosα>0,∴xy≤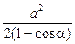 (当且仅当x=y时取“=”号),故此时谷仓的容积的最大值V1=(
(当且仅当x=y时取“=”号),故此时谷仓的容积的最大值V1=(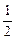 xysinα)b=
xysinα)b=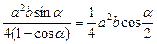
 同理,若木板短边着地时,谷仓的容积V的最大值V2=
同理,若木板短边着地时,谷仓的容积V的最大值V2=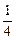 ab2cos
ab2cos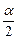 ,
,
∵a>b,∴V1>V2
从而当木板的长边着地,并且谷仓的底面是以a为底边的等腰三角形时,谷仓的容积最大,其最大值为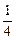 a2bcos
a2bcos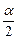 .
.

-2xycosα=2xy(1-cosα).
∵0<α<π,∴1-cosα>0,∴xy≤
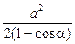 (当且仅当x=y时取“=”号),故此时谷仓的容积的最大值V1=(
(当且仅当x=y时取“=”号),故此时谷仓的容积的最大值V1=(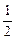 xysinα)b=
xysinα)b=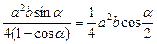
 同理,若木板短边着地时,谷仓的容积V的最大值V2=
同理,若木板短边着地时,谷仓的容积V的最大值V2=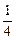 ab2cos
ab2cos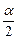 ,
,∵a>b,∴V1>V2
从而当木板的长边着地,并且谷仓的底面是以a为底边的等腰三角形时,谷仓的容积最大,其最大值为
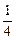 a2bcos
a2bcos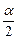 .
.
练习册系列答案
相关题目
 的不等式
的不等式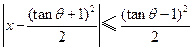 ,
,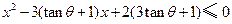 的解集分别为
的解集分别为 ,
, ,且
,且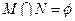 ,问这样的
,问这样的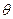 存在吗?若存在,求出
存在吗?若存在,求出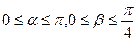 ,且
,且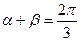 .
.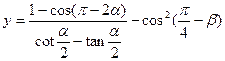 的最大值,并求出相应的
的最大值,并求出相应的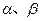 的值.
的值.
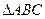 中,内角A、B、C的对边长分别为
中,内角A、B、C的对边长分别为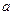 、
、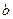 、
、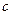 ,已知
,已知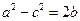 ,且
,且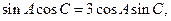 求b
求b 

 (
(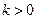 ).
). 函数
函数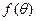 ;
;

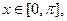 求函数
求函数 的值域; (Ⅱ)在
的值域; (Ⅱ)在 中,角A、B、C所对的边分别为a、b、c,若
中,角A、B、C所对的边分别为a、b、c,若


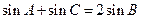 ,且
,且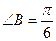 ,如果△ABC的面积为
,如果△ABC的面积为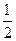 ,则
,则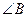 的对边b等于
的对边b等于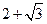
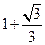
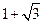
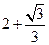
 ,则
,则 是( )
是( ) 的奇函数
的奇函数 的奇函数
的奇函数 的偶函数
的偶函数