题目内容
“a≥0”是“函数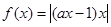 在区间(-∞,0)内单调递减”的( )
在区间(-∞,0)内单调递减”的( )
| A.充要条件 | B.必要不充分条件 |
C.充分不 必要条件 必要条件 | D.即不充分也不必要条件 |
A
解析试题分析:令t=(ax-1)x=ax2-x,则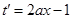 ,设
,设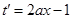 =0,解得x=
=0,解得x=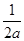 ,所以,当a≥0时,函数t=(ax-1)x在(-∞,
,所以,当a≥0时,函数t=(ax-1)x在(-∞,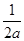 )上是减函数,在(
)上是减函数,在(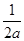 ,+∞)上是增函数,即极小值为-
,+∞)上是增函数,即极小值为- ,当x<0时,t>0,所以a≥0时,函数
,当x<0时,t>0,所以a≥0时,函数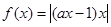 在区间(-∞,0)内单调递减;若函数
在区间(-∞,0)内单调递减;若函数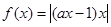 在区间(-∞,0)内单调递减,则x
在区间(-∞,0)内单调递减,则x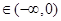 时,
时, <0,即
<0,即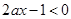 成立,所以2a ≥0,故选A.
成立,所以2a ≥0,故选A.
考点:1.导数的应用;2.充分必要条件的判断.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
“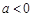 ”是“函数
”是“函数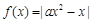 在区间
在区间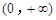 上单调递增”的
上单调递增”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列有关命题的说法正确的是 ( )
A.命题“若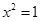 ,则 ,则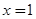 ”的否命题为:“若 ”的否命题为:“若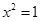 ,则 ,则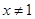 ”. ”. |
B.“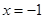 ”是“ ”是“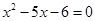 ”的必要不充分条件. ”的必要不充分条件. |
C.命题“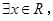 使得 使得 ”的否定是:“ ”的否定是:“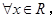 均有 均有 ”. ”. |
D.命题“若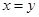 ,则 ,则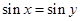 ”的逆否命题为真命题. ”的逆否命题为真命题. |
下列命题正确的是( )
A. | B. |
C. 是 是 的充分不必要条件 的充分不必要条件 | D.若 ,则 ,则 |
下列说法错误的是( )
A.若命题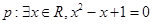 ,则 ,则 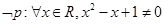 ; ; |
B.“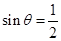 ”是“ ”是“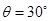 ”的充分不必要条件; ”的充分不必要条件; |
C.命题“若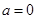 ,则 ,则 ”的否命题是:“若 ”的否命题是:“若 ,则 ,则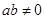 ”; ”; |
D.已知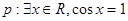 , ,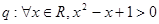 ,则“ ,则“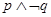 ”为假命题. ”为假命题. |
已知数列 ,那么“对任意的
,那么“对任意的 ,点
,点 都在直线
都在直线 上”是“
上”是“ 为等差数列”的 ( )
为等差数列”的 ( )
| A.必要而不充分条件 | B.既不充分也不必要条件 |
| C.充要条件 | D.充分而不必要条件 |
已知“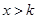 ”是“
”是“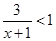 ”的充分不必要条件,则k的取值范围是( )
”的充分不必要条件,则k的取值范围是( )
A.[2,+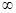 ) ) | B.[1,+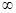 ) ) | C.(2,+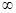 ) ) | D.(一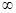 ,-1] ,-1] |
若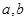 都是实数,则“
都是实数,则“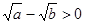 ”是“
”是“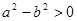 ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |