题目内容
19.设函数f(x)=x3-3ax2+3(2-a)x,a∈R(1)求f(x)的单调递增区间;
(2)若y=f(x)的图象与x轴相切于原点,且当x2<x1<4时,f(x1)=f(x2),求证:x1+x2>0.
分析 (1)先求导f′(x)=3x2-6ax+3(2-a),再确定△=36(a2+a-2)=36(a+2)(a-1);从而以△讨论单调区间即可;
(2)令f′(0)=3×02-6a•0+3(2-a)=0可求得a=2;从而化简f(x)=x3-6x2,从而可知f(x)的单调递增区间为(-∞,0),(4,+∞);单调减区间为(0,4);再由f(x1)=f(x2),且x2<x1<4知x2<0,x1>0,从而可得f(x2)>f(-x1),再由单调性可得x2>-x1,从而证明.
解答  解:(1)f′(x)=3x2-6ax+3(2-a),
解:(1)f′(x)=3x2-6ax+3(2-a),
△=36(a2+a-2)=36(a+2)(a-1);
①当a<-2或a>1时,
由f′(x)=3x2-6ax+3(2-a)=0解得,
x=a±$\sqrt{{a}^{2}+a-2}$;
f(x)的单调递增区间为(-∞,a-$\sqrt{{a}^{2}+a-2}$),(a+$\sqrt{{a}^{2}+a-2}$,+∞);
②当-2≤a≤1时,f(x)的单调递增区间为(-∞,+∞);
(2)证明:令f′(0)=3×02-6a•0+3(2-a)=0得a=2;
故f(x)=x3-6x2,
由(1)知,f(x)的单调递增区间为(-∞,0),(4,+∞);
单调减区间为(0,4);
∵f(x1)=f(x2),且x2<x1<4,
∴x2<0,x1>0,
则-x1<0,而f(x1)-f(-x1)=2x13>0,
则f(x1)>f(-x1),
则f(x2)>f(-x1),
又f(x)的单调递增区间为(-∞,0),
故x2>-x1,
故x1+x2>0.
点评 本题考查了导数的综合应用,二次方程的根及单调性的判断与应用,属于中档题.

练习册系列答案
相关题目
9.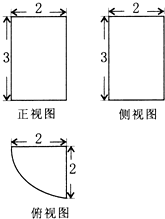 某空间几何体的三视图如图所示(其中俯视图的弧线为四分之一圆),则该几何体的表面积为( )
某空间几何体的三视图如图所示(其中俯视图的弧线为四分之一圆),则该几何体的表面积为( )
 某空间几何体的三视图如图所示(其中俯视图的弧线为四分之一圆),则该几何体的表面积为( )
某空间几何体的三视图如图所示(其中俯视图的弧线为四分之一圆),则该几何体的表面积为( )| A. | 5π+4 | B. | 14π+4 | C. | 5π+12 | D. | 14π+12 |
14.如图所示,已知PA⊥平面ABC,∠ABC=120°,PA=AB=BC=6,则PC等于( )
| A. | 6 | B. | 4 | C. | 12 | D. | 144 |