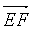题目内容
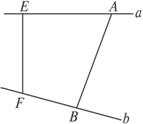
两条异面直线a、b间的距离是1cm，它们所成的角为60°，a、b上各有一点A，B，距公垂线的垂足都是10cm，则A、B两点间的距离为分析：先根据题意画出图形，再将异面直线所成角找出，注意分类讨论，构造直角三角形，解之即可．
解答：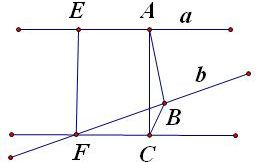
解：根据题意进行画图，
EF=1，EA=10，FB=10，∠CFB=60°，
将直线a平移到F，取FB=10，
当A，B在公垂线的同侧时，BC=10，AC=1，AC⊥BC，则AB=
当A，B在公垂线的异侧时，BC=10
，AC=1，AC⊥BC，则AB=
故答案为
或
解：根据题意进行画图，EF=1，EA=10，FB=10，∠CFB=60°，
将直线a平移到F，取FB=10，
当A，B在公垂线的同侧时，BC=10，AC=1，AC⊥BC，则AB=
| 101 |
当A，B在公垂线的异侧时，BC=10
| 3 |
| 301 |
故答案为
| 101 |
| 301 |
点评：本题主要考查了异面直线及其所成的角，以及余弦定理和两点间的距离公式的应用，属于基础题．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
α，b
平面β，a，b为两条异面直线．
·n B.| 
·n| C. 
·
D. 