题目内容
设函数 .
.
(1)设 ,
, ,
, ,证明:
,证明: 在区间
在区间 内存在唯一的零点;
内存在唯一的零点;
(2)设 ,若对任意
,若对任意 、
、 ,有
,有 ,求
,求 的取值范围.
的取值范围.
(1)详见解析;(2)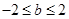 .
.
解析试题分析:(1)利用零点存在定理说明 在区间
在区间 内存在零点,然后利用函数
内存在零点,然后利用函数 的单调性来说明零点的唯一性;(2)先确定函数
的单调性来说明零点的唯一性;(2)先确定函数 的解析式,将问题等价转化为“
的解析式,将问题等价转化为“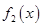 在
在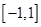 上的最大值与最小值之差
上的最大值与最小值之差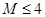 ”,对二次函数
”,对二次函数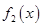 的对称轴与区间
的对称轴与区间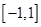 的位置关系来进行分类讨论,从而求解出实数
的位置关系来进行分类讨论,从而求解出实数 的取值范围.
的取值范围.
试题解析:(1)当 ,
, ,
, 时,
时, ,
,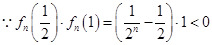 ,
,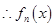 在区间
在区间 内存在零点,
内存在零点,
又当 时,
时,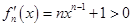 ,
,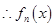 在区间
在区间 是单调递增的,
是单调递增的,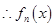 在区间
在区间 内存在唯一的零点;
内存在唯一的零点;
(2)当 时,
时,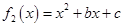 ,
,
对任意 、
、 都有
都有 等价于
等价于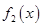 在
在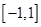 上的最大值与最小值之差
上的最大值与最小值之差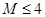 ,
,
据此分类讨论如下:
(i)当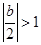 时,即
时,即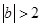 时,
时,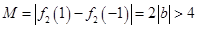 ,与题设矛盾!
,与题设矛盾!
(ii)当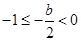 ,即
,即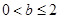 时,
时,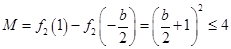 恒成立;
恒成立;
(iii)当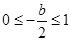 ,即
,即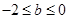 时,
时,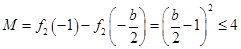 .
.
综上所述,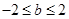 .
.
考点:1.零点存在定理;2.分类讨论

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为偶函数.
为偶函数. 的值;
的值; 有且只有一个根,求实数
有且只有一个根,求实数 的取值范围.
的取值范围. 为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为
为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为 ,对称轴与地面垂直,沟深2米,沟中水深1米.
,对称轴与地面垂直,沟深2米,沟中水深1米.

 满足
满足 ,当
,当 时,
时, ,且
,且 .
. 的值;
的值; 的方程
的方程 有解,求
有解,求 的取值范围.
的取值范围.
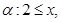 命题
命题 且命题
且命题 是
是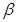 的必要条件,求实数m的取值范围
的必要条件,求实数m的取值范围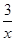 )元.
)元. (1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.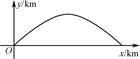
 AB,tan∠FED=
AB,tan∠FED= ,设AB=xm,BC=ym.
,设AB=xm,BC=ym.
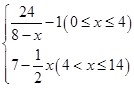 若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用.
若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用.