题目内容
(本小题满分12分)在△ABC中,BC= ,AC=3,sinC=2sinA.
,AC=3,sinC=2sinA.
(Ⅰ)求边长AB的值;
(Ⅱ)求△ABC的面积.
 ,AC=3,sinC=2sinA.
,AC=3,sinC=2sinA.(Ⅰ)求边长AB的值;
(Ⅱ)求△ABC的面积.
(1) (2)3
(2)3
 (2)3
(2)3试题分析:(1)解:在
 中,根据正弦定理,
中,根据正弦定理, , 2分
, 2分于是
 . .5分
. .5分(2)解:在
 中,根据余弦定理,
中,根据余弦定理,得

 , 8分
, 8分于是
 =
= , 10分
, 10分从而
 3 12分
3 12分点评:解决的关键是对于已知中的边角关系,结合正弦定理来得到边长,同时能结合余弦定理来得到角A,从而求解面积,属于基础题。

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 为
为 的三内角,且其对边分别为
的三内角,且其对边分别为 .若向量
.若向量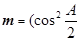 ,
, ,向量
,向量 ,
, ,且
,且 .
. 的值; (2)若
的值; (2)若 ,三角形面积
,三角形面积 ,求
,求 的值.
的值. 中,已知
中,已知 ,
, , ,求角
, ,求角 .经推断,破损处的条件为三角形的一边长度,且答案为
.经推断,破损处的条件为三角形的一边长度,且答案为 .将条件补充完整填在空白处.
.将条件补充完整填在空白处.  中,三边
中,三边 所对的角分别为
所对的角分别为 、
、 、
、 , 若
, 若 ,
, ,
, ,则
,则 。
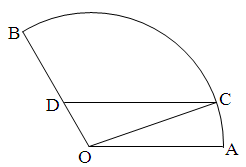
。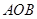 是一个观光区的平面示意图,其中
是一个观光区的平面示意图,其中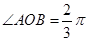 ,半径
,半径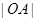 =1
=1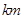 ,为了便于游客观光休闲,拟在观光区内铺设一条从入口
,为了便于游客观光休闲,拟在观光区内铺设一条从入口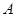 到出口
到出口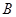 的观光道路,道路由弧
的观光道路,道路由弧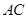 ,线段
,线段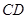 及线段
及线段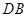 组成,其中
组成,其中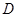 在线段
在线段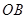 上且
上且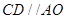 ,设
,设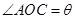
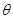 表示
表示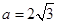 ,
,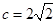 ,
,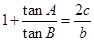 ,则角C大小为 。
,则角C大小为 。 -2
-2 -1)
-1) 中,
中,
 ,
,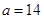 ,则
,则
 _______________.
_______________. 中,角
中,角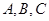 的对边分别为
的对边分别为 ,且满足
,且满足

 的大小;
的大小; 的取值范围。
的取值范围。