题目内容
【题目】函数 ![]() 是定义域为
是定义域为 ![]() 的偶函数,当
的偶函数,当 ![]() 时,
时, ![]() 若关于
若关于 ![]() 的方程
的方程 ![]()
![]() 有且仅有8个不同实数根,则实数
有且仅有8个不同实数根,则实数 ![]() 的取
的取
值范围是
【答案】![]()
【解析】当0≤x≤2时,y=- ![]() 递减,当x>2时,y=
递减,当x>2时,y= ![]() 递增,
递增,
由于函数y=f(x)是定义域为R的偶函数,
则f(x)在(-∞,-2)和(0,2)上递减,在(-2,0)和(2,+∞)上递增,
当x=0时,函数取得极大值0;当x=±2时,取得极小值-1.
当0≤x≤2时,y=- ![]() ∈[-1,0].
∈[-1,0].
当x>2时,y= ![]() ∈[-1,-
∈[-1,- ![]()
要使关于x的方程 ![]() ,有且仅有8个不同实数根,
,有且仅有8个不同实数根,
设t=f(x),则t2+at+ ![]() =0的两根均在(-1,-
=0的两根均在(-1,- ![]()
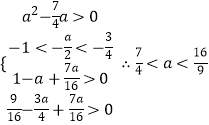
故答案为 ![]()
本题主要考查函数的单调性、奇偶性的应用以及函数的零点问题。根据题意先分析函数的单调性和值域,要使函数有8个不同实数根,转化为方程的两个根在(-1,- 3/ 4 )上,由二次方程根的分布即可列出不等式组进行求解即可。

练习册系列答案
相关题目