题目内容
已知不等式-1<
<1的解集是{x|-2<x<0},求a的值.
| ax-1 | x-1 |
分析:法一:利用不等式转化为二次不等式求解即可.
法二:不等式转化为分式不等式组,然后求解.
法三:转化不等式组,通过对a的讨论,直接求解不等式的解集即可.
法二:不等式转化为分式不等式组,然后求解.
法三:转化不等式组,通过对a的讨论,直接求解不等式的解集即可.
解答:法一:解:原是等价于
<1?(ax-1)2<(x-1)2,(x≠1)
?(a2-1)x2-2(a-1)x<0…(6分)
由解集{x|-2<x<0}知
方程(a2-1)x2-2(a-1)x=0的两根分别为-2和0,…(4分)
故(a2-1)(-2)2-2(a-1)(-2)=0且a2-1>0 解之得:a=-2 …(2分)
法二:原不等式等价于
(3分)
⇒
⇒
(3分)
⇒
(2分)
⇒a=-2(1分)
法三:-1<
<1⇒
(1分)
(1)当a=1时,不等式组无解;(2分)
(2)当a=-1时,
⇒x<0不符;(2分)
(3)当a>1时
⇒0<x<
不符;(2分)
(4)当-1<a<1时
⇒x<0或x>
不符;(2分)
(5)当a<-1时
⇒
<a<0,(2分)
∴
=-2,即a=-2.(1分)
(注:法1和法3作为基本思路)
| (ax-1)2 |
| (x-1)2 |
?(a2-1)x2-2(a-1)x<0…(6分)
由解集{x|-2<x<0}知
方程(a2-1)x2-2(a-1)x=0的两根分别为-2和0,…(4分)
故(a2-1)(-2)2-2(a-1)(-2)=0且a2-1>0 解之得:a=-2 …(2分)
法二:原不等式等价于
|
⇒
|
|
⇒
|
⇒a=-2(1分)
法三:-1<
| ax-1 |
| x-1 |
|
(1)当a=1时,不等式组无解;(2分)
(2)当a=-1时,
|
(3)当a>1时
|
| 2 |
| a+1 |
(4)当-1<a<1时
|
| 2 |
| a+1 |
(5)当a<-1时
|
| 2 |
| a+1 |
∴
| 2 |
| a+1 |
(注:法1和法3作为基本思路)
点评:本题考查不等式的求法,转化思想的应用,考查计算能力.

练习册系列答案
相关题目
已知不等式x-2≤
的解集为{x|x≤-1或0<x≤3},则实数a的值为( )
| a |
| x |
| A、-3 | B、-1 | C、1 | D、3 |
 或x>-
或x>-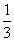 }
}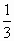 或x>
或x> }
}