题目内容
已知不等式x-2≤
的解集为{x|x≤-1或0<x≤3},则实数a的值为( )
| a |
| x |
| A、-3 | B、-1 | C、1 | D、3 |
分析:把不等式右边移项到左边,通分后设分子为0,得到关于x的方程,设出方程的两根为x1,x2,且x1<x2,在数轴上画出不等式的解集,由已知的解集得到x1与x2的值,利用韦达定理即可求出a的值.
解答:解:不等式x-2≤
变形为:
≤0,
设x2-2x-a=0的两根为x1,x2,且x1<x2,
其解集为:
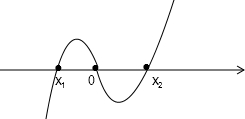
∴x1=-1,x2=3,
∴
,及-a=-1×3,
则a的值为3.
故选D
| a |
| x |
| x2-2x-a |
| x |
设x2-2x-a=0的两根为x1,x2,且x1<x2,
其解集为:

∴x1=-1,x2=3,
∴
|
则a的值为3.
故选D
点评:此题考查了其他不等式的解法,涉及的知识有方程解与不等式的关系,以及韦达定理,利用了转化及数形结合的思想.把原不等式适当变形后,设出令分子等于0时方程的两根,从而借助图形画出不等式的解集是解本题的关键.

练习册系列答案
相关题目