题目内容
(12分)已知椭圆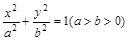 ,直线l与椭圆交于A、B两点,M是线段AB的中点,连接OM并延长交椭圆于点C.直线AB与直线OM的斜率分别为k、m,且
,直线l与椭圆交于A、B两点,M是线段AB的中点,连接OM并延长交椭圆于点C.直线AB与直线OM的斜率分别为k、m,且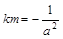 .
.

(Ⅰ)求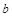 的值;
的值;
(Ⅱ)若直线AB经过椭圆的右焦点F,问:对于任意给定的不等于零的实数k,是否存在a∈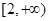 ,使得四边形OACB是平行四边形,请证明你的结论;
,使得四边形OACB是平行四边形,请证明你的结论;
【答案】
(1) 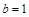
(2) 当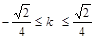 且
且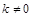 时,存在a∈[2,+∞],使得四边形OACB是平行四边形;
时,存在a∈[2,+∞],使得四边形OACB是平行四边形;
当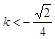 或
或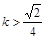 时,不存在a∈[2,+∞],使得四边形OACB是平行四边形
时,不存在a∈[2,+∞],使得四边形OACB是平行四边形
【解析】解:(Ⅰ)解法一:设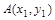 ,
,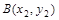 ,
,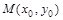 ,
,
则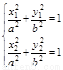 ,两式相减,得:
,两式相减,得: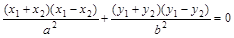 ,
,
又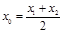 ,
,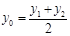 ,∴
,∴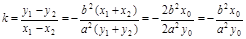 ,
,
又∵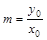 ,
,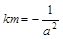 ∴
∴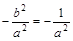 ,∴
,∴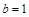 …4分
…4分
解法二:设直线AB的方程为y=kx+n,代入椭圆方程得
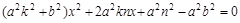 ,设
,设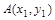 ,
,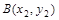 ,
,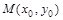 ,
,
则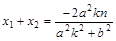 ,∴
,∴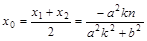 ,
,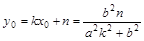 ,
,
∴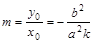 ,又
,又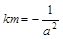 ∴
∴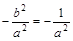 ,∴
,∴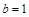 ……4分
……4分
(Ⅱ)设C(xC,yC),直线AB的方程为y=k(x-c)(k≠0),代入椭圆方程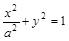 ,
,
得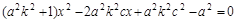 ,若OACB是平行四边形,则
,若OACB是平行四边形,则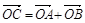 ,
,
∴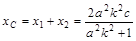 ,
,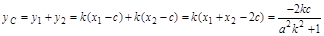 ,
,
∵C在椭圆上 ∴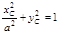 ∴
∴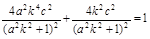 ,
,
∴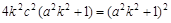 ,∴
,∴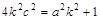 ∴
∴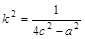 ,
,
∵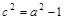 ,a∈[2,+∞] ,∴
,a∈[2,+∞] ,∴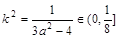 ,∴
,∴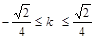 且
且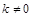 ,
,
∴当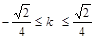 且
且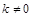 时,存在a∈[2,+∞],使得四边形OACB是平行四边形;
时,存在a∈[2,+∞],使得四边形OACB是平行四边形;
当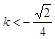 或
或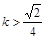 时,不存在a∈[2,+∞],使得四边形OACB是平行四边形。……12分
时,不存在a∈[2,+∞],使得四边形OACB是平行四边形。……12分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,F1,F2为椭圆C:
如图,F1,F2为椭圆C: 过点
过点 ,离心率
,离心率 ,若点M(x,y)在椭圆C上,则点
,若点M(x,y)在椭圆C上,则点 称为点M的一个“椭点”,直线l交椭圆C于A、B两点,若点A、B的“椭点”分别是P、Q,且以PQ为直径的圆经过坐标原点O.
称为点M的一个“椭点”,直线l交椭圆C于A、B两点,若点A、B的“椭点”分别是P、Q,且以PQ为直径的圆经过坐标原点O.