题目内容
某同学在学习时发现，以下五个式子的值都等于同一个常数M：
sin213°+cos217°-sin13°cos17°
sin215°+cos215°-sin15°cos15°
sin218°+cos212°-sin18°cos12°
sin218°+cos248°+sin18°cos48°
sin225°+cos255°+sin25°cos55°
（1）M=
；
（2）根据（1）的计算结果，将该同学的发现推广为三角恒等式为：
sin213°+cos217°-sin13°cos17°
sin215°+cos215°-sin15°cos15°
sin218°+cos212°-sin18°cos12°
sin218°+cos248°+sin18°cos48°
sin225°+cos255°+sin25°cos55°
（1）M=
| 3 |
| 4 |
| 3 |
| 4 |
（2）根据（1）的计算结果，将该同学的发现推广为三角恒等式为：
sin2（α-30°）+cos2α+sin（α-30°）cosα=
| 3 |
| 4 |
sin2（α-30°）+cos2α+sin（α-30°）cosα=
．| 3 |
| 4 |
分析：先利用一个式子，利用三角函数的公式计算出常数值，根据已知两个式子的特点寻找规律即可．
解答：解：（1）sin215°+cos215°-sin15°cos15°=1--
sin30?=1-
=
．
所以常数为
．
（2）由这几个式子可知，前后两个角相差30°，故根据归纳推理可得：
sin2（α-30°）+cos2α+sin（α-30°）cosα=
．
故答案为：
；sin2（α-30°）+cos2α+sin（α-30°）cosα=
．
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
所以常数为
| 3 |
| 4 |
（2）由这几个式子可知，前后两个角相差30°，故根据归纳推理可得：
sin2（α-30°）+cos2α+sin（α-30°）cosα=
| 3 |
| 4 |
故答案为：
| 3 |
| 4 |
| 3 |
| 4 |
点评：本题主要考查归纳推理的应用，要求熟练掌握．
练习册系列答案
相关题目
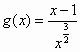的图像的下方，试问：他的判断是否正确？若正确，请说明理由：若不正确，请给出你的正确判断；