题目内容
某研究性学习小组研究函数y=lnx上的点P(x,y)与原点o的连线所在的直线的斜率k的值的变化规律.记直线OP的斜率k=f(x).
(I)某同学甲发现:点P从左向右运动时,f(x)不断增大,试问:他的判断是否正确?若正确,请说明理由:若不正确,请给出你的正确判断;
(Ⅱ)某同学乙发现:总存在正实数a、b(a<b),使ab=ba.试问:他的判断是否正确?若不正确,请说明理由:若正确,请求出a的取值范围;
(III)某同学丙发现:当x>1时,函数k=f(x)的图象总在函数g(x)=
的图象的下方,试问:他的判断是否正确?若正确,请说明理由:若不正确,请给出你的正确判断.
(I)某同学甲发现:点P从左向右运动时,f(x)不断增大,试问:他的判断是否正确?若正确,请说明理由:若不正确,请给出你的正确判断;
(Ⅱ)某同学乙发现:总存在正实数a、b(a<b),使ab=ba.试问:他的判断是否正确?若不正确,请说明理由:若正确,请求出a的取值范围;
(III)某同学丙发现:当x>1时,函数k=f(x)的图象总在函数g(x)=
| x-1 | ||
x
|
分析:(I)某同学甲的判断不正确,理由为:f(x)=
,f′(x)=
,利用f'(x)的符号,可得f(x)的单调性.
(Ⅱ)同学乙的判断正确,理由为:x→+∞时,f(x)=
→0,且
>0(x>e),由图象可得总存在正实数a、b且1<a<e<b,使得f(a)=f(b),由此求得实数a的取值范围.
(III)同学丙的判断正确:由f(x)-
=
-
=
,记g(x)=lnx-
+
,由g′(x)的符号可得g(x)的单调性,根据g(x)的单调性可得g(x)<0,
f(x)-
<0,即 f(x)<
.
| lnx |
| x |
| 1-lnx |
| x2 |
(Ⅱ)同学乙的判断正确,理由为:x→+∞时,f(x)=
| lnx |
| x |
| lnx |
| x |
(III)同学丙的判断正确:由f(x)-
| x-1 | ||
x
|
| lnx |
| x |
| x-1 | ||
x
|
lnx-
| ||||||
| x |
| x |
| 1 | ||
|
f(x)-
| x-1 | ||
x
|
| x-1 | ||
x
|
解答: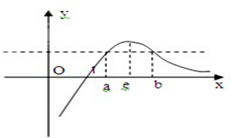 解:(I)某同学甲的判断不正确.
解:(I)某同学甲的判断不正确.
依题意可得,f(x)=
,f′(x)=
,
当x∈(0,e)时,f'(x)>0;当x∈(e,+∞)时,f'(x)<0.
所以,f(x)在(0,e)上递增,在(e,+∞)上递减. …(4分)
(Ⅱ)同学乙的判断正确.
∵当x→+∞时,f(x)=
→0,
且
>0(x>e),又由(1)得f(x)的图象如图所示
所以总存在正实数a、b且1<a<e<b,
使得f(a)=f(b)即
=
也就是 ab=ba,
此时实数a的取值范围为(1,e).…(9分)
(III)同学丙的判断正确:问题等价于求证:当x>1时,f(x)<
成立.
∵f(x)-
=
-
=
,记g(x)=lnx-
+
,
g′(x)=
-
x-
-
x-
=
x-
(2
-x-1)=-
x-
(
-1)2<0,
所以g(x)在(1,+∞)上为减函数,则 g(x)=lnx-
+
<g(1)=0,
所以 f(x)-
<0,即 f(x)<
,
∴当x>1时,函数k=f(x)的图象总在函数g(x)=
的图象的下方. …(14分)
 解:(I)某同学甲的判断不正确.
解:(I)某同学甲的判断不正确.依题意可得,f(x)=
| lnx |
| x |
| 1-lnx |
| x2 |
当x∈(0,e)时,f'(x)>0;当x∈(e,+∞)时,f'(x)<0.
所以,f(x)在(0,e)上递增,在(e,+∞)上递减. …(4分)
(Ⅱ)同学乙的判断正确.
∵当x→+∞时,f(x)=
| lnx |
| x |
且
| lnx |
| x |
所以总存在正实数a、b且1<a<e<b,
使得f(a)=f(b)即
| lna |
| a |
| lnb |
| b |
此时实数a的取值范围为(1,e).…(9分)
(III)同学丙的判断正确:问题等价于求证:当x>1时,f(x)<
| x-1 | ||
x
|
∵f(x)-
| x-1 | ||
x
|
| lnx |
| x |
| x-1 | ||
x
|
lnx-
| ||||||
| x |
| x |
| 1 | ||
|
g′(x)=
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| x |
| 1 |
| 2 |
| 3 |
| 2 |
| x |
所以g(x)在(1,+∞)上为减函数,则 g(x)=lnx-
| x |
| 1 | ||
|
所以 f(x)-
| x-1 | ||
x
|
| x-1 | ||
x
|
∴当x>1时,函数k=f(x)的图象总在函数g(x)=
| x-1 | ||
x
|
点评:本题主要考查利用导数研究函数的单调性,对数函数的图象性质的应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某研究性学习小组研究函数f(x)=ax3+bx(a≠0,a,b为常数)的 性质:
(Ⅰ)甲同学得到如下表所示的部分自变量x及其对应函数值y的近似值(精确到0.01):
请你根据上述表格中的数据回答下列问题:
(i)函数f(x)在区间(0.4,0.44)内是否存在零点,写出你的判断并加以证明;
(ii)证明:函数f(x)在区间(-∞,-0.3)上单调递减;
(Ⅱ)乙同学发现对于函数f(x)图象上的两点A(-1,4),B(t,f(t))(-1<t<2),存在m∈(-1,t),使f'(m)的值恰为直线AB的斜率,请你判断乙同学的结论是否正确?若正确,请给出证明并确定m的个数,若不正确,请说明理由.
(Ⅰ)甲同学得到如下表所示的部分自变量x及其对应函数值y的近似值(精确到0.01):
| x | -1 | -0.72 | -0.44 | -0.16 | 0.12 | 0.4 |
| y的近似值 | 4.00 | 1.15 | 0.02 | -0.14 | 0.11 | 0.08 |
(i)函数f(x)在区间(0.4,0.44)内是否存在零点,写出你的判断并加以证明;
(ii)证明:函数f(x)在区间(-∞,-0.3)上单调递减;
(Ⅱ)乙同学发现对于函数f(x)图象上的两点A(-1,4),B(t,f(t))(-1<t<2),存在m∈(-1,t),使f'(m)的值恰为直线AB的斜率,请你判断乙同学的结论是否正确?若正确,请给出证明并确定m的个数,若不正确,请说明理由.
某研究性学习小组研究函数f(x)=ax3+bx(a≠0,a,b为常数)的 性质:
(Ⅰ)甲同学得到如下表所示的部分自变量x及其对应函数值y的近似值(精确到0.01):
| x | -1 | -0.72 | -0.44 | -0.16 | 0.12 | 0.4 |
| y的近似值 | 4.00 | 1.15 | 0.02 | -0.14 | 0.11 | 0.08 |
(i)函数f(x)在区间(0.4,0.44)内是否存在零点,写出你的判断并加以证明;
(ii)证明:函数f(x)在区间(-∞,-0.3)上单调递减;
(Ⅱ)乙同学发现对于函数f(x)图象上的两点A(-1,4),B(t,f(t))(-1<t<2),存在m∈(-1,t),使f'(m)的值恰为直线AB的斜率,请你判断乙同学的结论是否正确?若正确,请给出证明并确定m的个数,若不正确,请说明理由.
某研究性学习小组研究函数f(x)=ax3+bx(a≠0,a,b为常数)的 性质:
(Ⅰ)甲同学得到如下表所示的部分自变量x及其对应函数值y的近似值(精确到0.01):
请你根据上述表格中的数据回答下列问题:
(i)函数f(x)在区间(0.4,0.44)内是否存在零点,写出你的判断并加以证明;
(ii)证明:函数f(x)在区间(-∞,-0.3)上单调递减;
(Ⅱ)乙同学发现对于函数f(x)图象上的两点A(-1,4),B(t,f(t))(-1<t<2),存在m∈(-1,t),使f'(m)的值恰为直线AB的斜率,请你判断乙同学的结论是否正确?若正确,请给出证明并确定m的个数,若不正确,请说明理由.
(Ⅰ)甲同学得到如下表所示的部分自变量x及其对应函数值y的近似值(精确到0.01):
| x | -1 | -0.72 | -0.44 | -0.16 | 0.12 | 0.4 |
| y的近似值 | 4.00 | 1.15 | 0.02 | -0.14 | 0.11 | 0.08 |
(i)函数f(x)在区间(0.4,0.44)内是否存在零点,写出你的判断并加以证明;
(ii)证明:函数f(x)在区间(-∞,-0.3)上单调递减;
(Ⅱ)乙同学发现对于函数f(x)图象上的两点A(-1,4),B(t,f(t))(-1<t<2),存在m∈(-1,t),使f'(m)的值恰为直线AB的斜率,请你判断乙同学的结论是否正确?若正确,请给出证明并确定m的个数,若不正确,请说明理由.
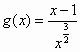 的图像的下方,试问:他的判断是否正确?若正确,请说明理由:若不正确,请给出你的正确判断;
的图像的下方,试问:他的判断是否正确?若正确,请说明理由:若不正确,请给出你的正确判断;