题目内容
下面玩掷骰子放球的游戏:若掷出1点,甲盒中放入一球;若掷出2点或是3点,乙盒中放入一球;若掷出4点或5点或6点,丙盒中放入一球.设掷n次后,甲、乙、丙盒内的球数分别为x,y,z.
(1)当n=3时,求x、y、z成等差数列的概率;
(2)当n=6时,求x、y、z成等比数列的概率;
(3)设掷4次后,甲盒和乙盒中球的个数差的绝对值为ξ,求Eξ.
(1)当n=3时,求x、y、z成等差数列的概率;
(2)当n=6时,求x、y、z成等比数列的概率;
(3)设掷4次后,甲盒和乙盒中球的个数差的绝对值为ξ,求Eξ.
(1)因为x+y+z=3,且2y=x+z,
所以或,或.
当x=0,y=1,z=2时,只投掷3次出现1次2点或3点、2次4点或5点或6点,即此时的概率为C·0·1·2=.
当x=1,y=1,z=1时,只投掷3次出现1次1点、1次2点或是3点、1次4点或5点或6点,即此时的概率为C·C·1·1·1=.
当x=2,y=1,z=0时,只投掷3次出现2次1点、1次2点或3点,即此时的概率为C·2·1·0=.
故当n=3时,x,y,z成等差数列的概率为++=.
(2)当n=6,且x,y,z成等比数列时,由x+y+z=6,且y2=xz,得x=y=z=2.
此时概率为C·2·C·2·C·2=.
(3)ξ的可能值为0,1,2,3,4.
P(ξ=0)=4+C1C1C2+C2C2=;
P(ξ=1)=C13+C13+C2C1C1+C1C2C1=;
P(ξ=2)=C22+C22+C31+C13=;
P(ξ=3)=C31+C31=;
P(ξ=4)=C4+C4=;
Eξ=×0+×1+×2+×3+×4=
所以或,或.
当x=0,y=1,z=2时,只投掷3次出现1次2点或3点、2次4点或5点或6点,即此时的概率为C·0·1·2=.
当x=1,y=1,z=1时,只投掷3次出现1次1点、1次2点或是3点、1次4点或5点或6点,即此时的概率为C·C·1·1·1=.
当x=2,y=1,z=0时,只投掷3次出现2次1点、1次2点或3点,即此时的概率为C·2·1·0=.
故当n=3时,x,y,z成等差数列的概率为++=.
(2)当n=6,且x,y,z成等比数列时,由x+y+z=6,且y2=xz,得x=y=z=2.
此时概率为C·2·C·2·C·2=.
(3)ξ的可能值为0,1,2,3,4.
P(ξ=0)=4+C1C1C2+C2C2=;
P(ξ=1)=C13+C13+C2C1C1+C1C2C1=;
P(ξ=2)=C22+C22+C31+C13=;
P(ξ=3)=C31+C31=;
P(ξ=4)=C4+C4=;
Eξ=×0+×1+×2+×3+×4=
略

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 .
. ,试写出
,试写出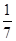
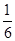
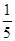
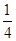
 ;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为
;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为 ,
, .
. 的数学期望;
的数学期望;
 的分布列及期望.
的分布列及期望. ,现甲共投5个球,规定每投篮一次命中得3分,未命中得-1分,则甲在5次投篮中所得分数的数学期望为 ▲ 分
,现甲共投5个球,规定每投篮一次命中得3分,未命中得-1分,则甲在5次投篮中所得分数的数学期望为 ▲ 分 服从正态分布
服从正态分布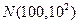 . 已知
. 已知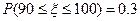 ,估计该班数学成绩在110分以上的人数为______________.
,估计该班数学成绩在110分以上的人数为______________. 表示摸出2个小球的标号之和,写出
表示摸出2个小球的标号之和,写出 .
.