题目内容
函数f(x)=sin(ωx+φ)(x∈R)(ω>0,|φ|<
)的部分图象如图所示,如果x1,x2∈(-
,
),且f(x1)=f(x2),则f(x1+x2)=( )

| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
A.
| B.
| C.
| D.1 |

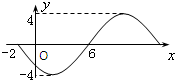
由图知,T=2×(
+
)=π,
∴ω=2,因为函数的图象经过(-
,0),0=sin(-
+ϕ)
∵|ϕ|<
,所以ϕ=
,
∴f(x)=sin(2x+
),x1+x2=2×
=
,
所以f(x1+x2)=sin
=
.
故选C.
| π |
| 3 |
| π |
| 6 |
∴ω=2,因为函数的图象经过(-
| π |
| 6 |
| π |
| 3 |
∵|ϕ|<
| π |
| 2 |
| π |
| 3 |
∴f(x)=sin(2x+
| π |
| 3 |
| π |
| 12 |
| π |
| 6 |
所以f(x1+x2)=sin
| 2π |
| 3 |
| ||
| 2 |
故选C.

练习册系列答案
相关题目


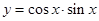 是( ).
是( ). ,那么
,那么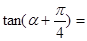 ( ).
( ).