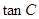题目内容
(1)已知sin(3π+α)=(2)已知![]() ,求
,求![]() 的值.
的值.
(3)已知方程sin(α-3π)=2cos(α-4π),求 的值.
的值.
(4)已知tan(π-α)=a2,|cos(π-α)|=-cosα,求![]() 的值.
的值.
思路分析:考查诱导公式和同角三角函数关系式的应用.前三个可以利用诱导公式和同角三角函数关系式将条件和所求的式子化简.而(4)除了化简之外,还应判断角终边的位置.
解:(1)∵sin(3π+α)=sin(π+α)=-sinα,∴sinα=![]() .
.
∴原式=![]() .
.
(2)![]() .
.
(3)∵sin(α-3π)=2cos(α-4π),
∴-sin(3π-α)=2cos(4π-α).
∴-sin(π-α)=2cos(-α).
∴sinα=-2cosα,且cosα≠0.
∴原式=![]() .
.
(4)由题设,tanα=-a2≤0,|cosα|=-cosα,即cosα≤0.
由此,当a≠0时,tanα<0,cosα<0,α为第二象限角,
∴原式=![]() .
.
当a=0时,tanα=0,α=kπ,∴cosα=±1.
∵cosα≤0,∴cosα=-1.
∴原式=![]() (a=0).
(a=0).
综上所述:![]() .
.
方法归纳 三角函数中角的变换是个难点,三角函数中的许多问题正是通过挖掘角与角之间的内在联系而解决的.而化简求值要遵循“负化正,大化小”的原则.
深化升华 本题是一个化简求值的题型,它的特点是已知一个复杂的等式,求另一个复杂的式子的值.解决这类问题的策略是:化简,化简,再化简.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
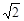 cos(
cos( +β),
+β),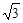 cos(-α)=-
cos(-α)=-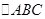 中,
中,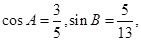 求
求