题目内容
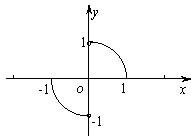 函数y=f(x)的图象是圆心在原点的单位圆的两段弧(如图),则不等式f(x)<f(-x)+2x的解集为( )
函数y=f(x)的图象是圆心在原点的单位圆的两段弧(如图),则不等式f(x)<f(-x)+2x的解集为( )A、{x|-
| ||||||||
B、{x|-1≤x<-
| ||||||||
C、{x|-1≤x<-
| ||||||||
D、{x|-
|
分析:根据图象得知是奇函数,据此将“不等式f(x)<f(-x)+2x”转化为“f(x)<x”,再令y=f(x),y=x,利用图象求解.
解答: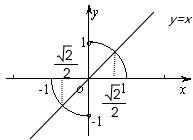 解:如图所示:函数是奇函数
解:如图所示:函数是奇函数
∴不等式f(x)<f(-x)+2x可转化为:f(x)<x,
令y=f(x),y=x
如图所示:{x|-
<x<0或
<x≤1}
故选A.
 解:如图所示:函数是奇函数
解:如图所示:函数是奇函数∴不等式f(x)<f(-x)+2x可转化为:f(x)<x,
令y=f(x),y=x
如图所示:{x|-
| ||
| 2 |
| ||
| 2 |
故选A.
点评:本题主要考查利用函数图象的相对位置关系来解不等式,关键是转化为特定的基本函数,能画其图象.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示,给出关于f(x)的下列命题:
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示,给出关于f(x)的下列命题: