题目内容
椭圆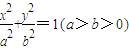 的一个焦点是F(1,0),已知椭圆短轴的两个三等分点与一个焦点构成正三角形.
的一个焦点是F(1,0),已知椭圆短轴的两个三等分点与一个焦点构成正三角形.(1)求椭圆的标准方程;
(2)已知Q(x,y)为椭圆上任意一点,求以Q为切点,椭圆的切线方程.
(3)设点P为直线x=4上一动点,过P作椭圆两条切线PA,PB,求证直线AB过定点,并求出该定点的坐标.
【答案】分析:(1)先由题意可得,△EFG为边长是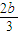 ,高为c=1的等边三角形.利用三角函数知识得出
,高为c=1的等边三角形.利用三角函数知识得出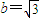 ,从而求得a值,最后写出椭圆的标准方程;
,从而求得a值,最后写出椭圆的标准方程;
(2)设以Q为切点的切线方程的斜率为k,再分类讨论:
①若y>0,设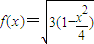 ,利用导数的几何求得切线的斜率进而得出切线方程;
,利用导数的几何求得切线的斜率进而得出切线方程;
②若y<0,设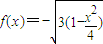 ,同理可得切线方程为
,同理可得切线方程为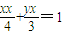 ;
;
③若y=0,则Q(2,0),切线方程为x=2,亦满足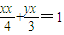 ,综上所述,得出切线方程.
,综上所述,得出切线方程.
(3)设点P(4,t),切点A(x1,y1),B(x2,y2),由(2)可知两切线方程PA,PB的方程,同去利用P点在切线PA,PB上,得到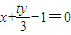 为AB的直线方程,从而问题解决.
为AB的直线方程,从而问题解决.
解答:解:(1)由题意可得,△EFG为边长是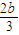 ,高为c=1的等边三角形.
,高为c=1的等边三角形.
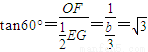 ,故
,故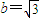 ,而c=1,所以
,而c=1,所以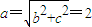
椭圆的标准方程为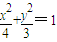 (3分)
(3分)
(2)设以Q为切点的切线方程的斜率为k,
①若y>0,设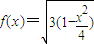 ,
,
则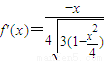 ,
,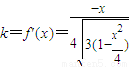
由于Q(x,y)在椭圆上,故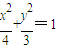 ,
,
即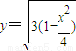 ∴
∴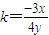
此时切线方程为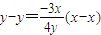 ,整理得:
,整理得: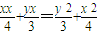
将 代入,得
代入,得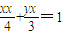 (6分)
(6分)
②若y<0,设 ,
,
则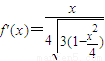 ,
,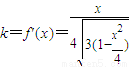
由于Q(x,y)在椭圆上,故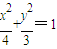 ,
,
即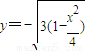 ∴
∴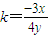
于是与①同理可得切线方程为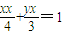 (8分)
(8分)
③若y=0,则Q(2,0),切线方程为x=2,亦满足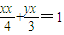
综上所述,切线方程为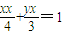 (9分)
(9分)
(3)设点P(4,t),切点A(x1,y1),B(x2,y2),
由(2)可知两切线方程PA,PB分别为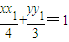 ,
, (11分)
(11分)
P点在切线PA,PB上,故P(4,t)满足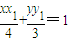 ,
,
得: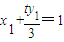 ,
,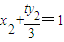
故A(x1,y1),B(x2,y2)均满足方程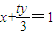 ,
,
即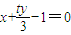 为AB的直线方程.(13分)
为AB的直线方程.(13分)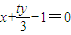 中,
中,
令y=0,则x=1,故AB过定点(1,0),题得证.(14分)
点评:本题主要考查椭圆的简单性质、直线与椭圆的位置关系,导数的几何意义等基本知识,考查运算能力和综合解题能力.解题时要注意运算能力的培养.
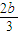 ,高为c=1的等边三角形.利用三角函数知识得出
,高为c=1的等边三角形.利用三角函数知识得出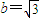 ,从而求得a值,最后写出椭圆的标准方程;
,从而求得a值,最后写出椭圆的标准方程;(2)设以Q为切点的切线方程的斜率为k,再分类讨论:
①若y>0,设
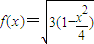 ,利用导数的几何求得切线的斜率进而得出切线方程;
,利用导数的几何求得切线的斜率进而得出切线方程;②若y<0,设
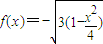 ,同理可得切线方程为
,同理可得切线方程为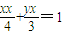 ;
;③若y=0,则Q(2,0),切线方程为x=2,亦满足
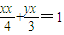 ,综上所述,得出切线方程.
,综上所述,得出切线方程.(3)设点P(4,t),切点A(x1,y1),B(x2,y2),由(2)可知两切线方程PA,PB的方程,同去利用P点在切线PA,PB上,得到
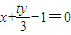 为AB的直线方程,从而问题解决.
为AB的直线方程,从而问题解决.解答:解:(1)由题意可得,△EFG为边长是
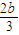 ,高为c=1的等边三角形.
,高为c=1的等边三角形.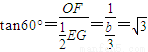 ,故
,故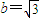 ,而c=1,所以
,而c=1,所以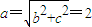
椭圆的标准方程为
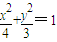 (3分)
(3分)(2)设以Q为切点的切线方程的斜率为k,
①若y>0,设
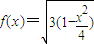 ,
,则
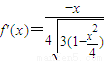 ,
,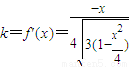
由于Q(x,y)在椭圆上,故
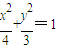 ,
,即
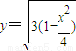 ∴
∴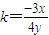
此时切线方程为
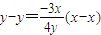 ,整理得:
,整理得: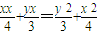
将
 代入,得
代入,得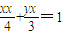 (6分)
(6分)②若y<0,设
 ,
,则
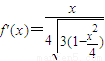 ,
,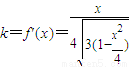
由于Q(x,y)在椭圆上,故
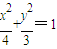 ,
,即
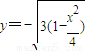 ∴
∴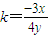
于是与①同理可得切线方程为
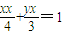 (8分)
(8分)③若y=0,则Q(2,0),切线方程为x=2,亦满足
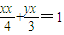
综上所述,切线方程为
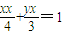 (9分)
(9分)(3)设点P(4,t),切点A(x1,y1),B(x2,y2),
由(2)可知两切线方程PA,PB分别为
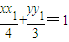 ,
, (11分)
(11分)P点在切线PA,PB上,故P(4,t)满足
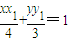 ,
,
得:
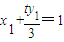 ,
,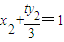
故A(x1,y1),B(x2,y2)均满足方程
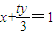 ,
,即
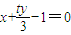 为AB的直线方程.(13分)
为AB的直线方程.(13分)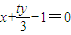 中,
中,令y=0,则x=1,故AB过定点(1,0),题得证.(14分)
点评:本题主要考查椭圆的简单性质、直线与椭圆的位置关系,导数的几何意义等基本知识,考查运算能力和综合解题能力.解题时要注意运算能力的培养.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 的一个焦点是F(1,0),O为坐标原点。
的一个焦点是F(1,0),O为坐标原点。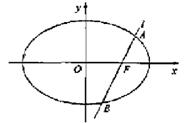
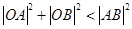 ,求a的取值范围。
,求a的取值范围。