题目内容
(1)如图,在Rt△ABC中,AB=BC,E、F分别是AC和AB的中点,以EF为棱把它折成大小为β的二面角A-EF-B,设∠AEC=α.求证:cosα=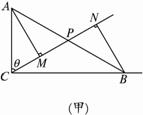
(2)Rt△ABC的两直角边AC=2,BC=3,P为斜边AB上一点.现沿CP将直角三角形折成直二面角A-PC-B,当AB=![]() 时,求二面角P-AC-B的大小.
时,求二面角P-AC-B的大小.
(1)证明:设AF=FB=a,∴AE=EC=![]() a,BC=2a.?
a,BC=2a.?
∵EF⊥AF,EF⊥FB,∴∠AFB=β,EF⊥面AFB.?
∴EF⊥AB.
∵EF∥BC,∴AB⊥BC.?
∴AB2=AC2-BC2.?
∵AB2=2a2(1-cosβ),?
AC2=2(![]() α)2(1-cosα),BC2=4a2,?
α)2(1-cosα),BC2=4a2,?
∴代入得cosα=![]() (cosβ-1).?
(cosβ-1).?
(2)解析:如图,过A作AM⊥PC于M,过B作BN⊥PC,设∠ACP=θ,∴AM=2sinθ,CN=3sinθ,BN=3cosθ.过B作BE1∥MN,过M作ME⊥BE1于E,连结AE.?

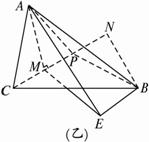
∵APCB为直二面角,?
∴BN⊥面ACP.?
∴△ACN为△ACB在面ACP上的射影.?
∵∠AME=90°,?
又∵ME⊥BE1,BE1∥MN,BN⊥MN,∴MEBN为矩形.?
∴ME=BN=3cosθ.?
∴AE2=4sin2θ+9cos2θ=4+5cos2θ.?
∵AM⊥EB,ME⊥EB,?
∴EB⊥面AME.∴EB⊥AE.?
∴AB2=AE2+EB2.?
∴7=4+5cos2θ+(3sinθ-2cosθ)2.?
∴sin2θ=1,θ=45°.?
∴S△CAN =![]() AM×CN=3sin2θ=
AM×CN=3sin2θ=![]() ,S△ACB?=
,S△ACB?=![]() ×BC×hBC=
×BC×hBC=![]() ×3×
×3×![]() =
=![]() .?
.?
设P-AC-B大小为β,?
∴cosβ=![]() .?
.?
∴β=arccos![]() =arctan
=arctan![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
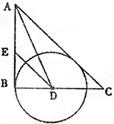 16、如图,在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,E为AB上一点,DE=DC,以D为圆心,以DB的长为半径画圆.
16、如图,在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,E为AB上一点,DE=DC,以D为圆心,以DB的长为半径画圆.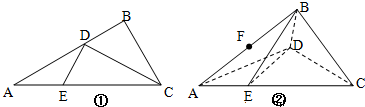
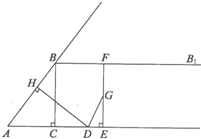 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.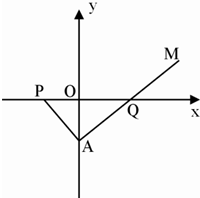 如图,在Rt△PAQ中,点P的坐标为(-8,0),点A在y轴上,点Q在x轴的正半轴上,∠PAQ=90°,在AQ的延长线上取一点M,使|AQ|=|MQ|.
如图,在Rt△PAQ中,点P的坐标为(-8,0),点A在y轴上,点Q在x轴的正半轴上,∠PAQ=90°,在AQ的延长线上取一点M,使|AQ|=|MQ|.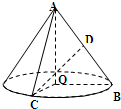 如图,在 Rt△AOB中,
如图,在 Rt△AOB中,