题目内容
(16分)已知函数![]() (
(![]() ∈R且
∈R且![]() ),
),![]() .
.
(Ⅰ)若![]() ,且函数
,且函数![]() 的值域为[0, +
的值域为[0, +![]() ),求
),求![]() 的解析式;
的解析式;
(Ⅱ)在(Ⅰ)的条件下,当x∈[-2 , 2 ]时,![]() 是单调函数,求实数k的取值范围;
是单调函数,求实数k的取值范围;
(Ⅲ)设![]() ,
,![]() , 且
, 且![]() 是偶函数,判断
是偶函数,判断![]() 能否大于零?
能否大于零?
解:(Ⅰ)![]()
∵函数![]() 的值域为[0, +
的值域为[0, +![]() ) ∴
) ∴![]() 且△=
且△=![]() ∴
∴![]()
∴
(Ⅱ)![]()
在定义域x∈[-2 , 2 ]上是单调函数,对称轴为![]()
∴![]() 或
或![]() 即
即![]() 或
或![]()
(Ⅲ)∵![]() 是偶函数 ∴
是偶函数 ∴![]()
∴![]() ∴
∴![]() ∴
∴![]()
∴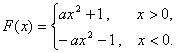
∵![]() 不妨设
不妨设![]() , 则
, 则![]() ,
,![]() ,
,
∴![]()
![]()
∵![]() ,
,![]() ,
,![]() ∴
∴![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
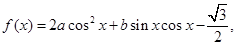 x∈R且
x∈R且 ,
,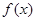 的最小正周期;
的最小正周期;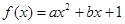 (
(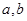 ∈R且
∈R且 ),
),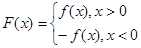 .
. ,且函数
,且函数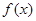 的值域为[0, +
的值域为[0, +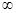 ),求
),求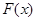 的解析式;
的解析式; 是单调函数,求实数k的取值范围;
是单调函数,求实数k的取值范围;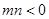 ,
,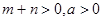 , 且
, 且 是否大于零?
是否大于零? (
(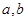 ∈R且
∈R且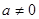 ),
),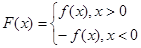 .
. ,且函数
,且函数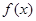 的值域为[0, +
的值域为[0, +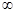 ),求
),求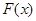 的解析式;
的解析式;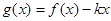 是单调函数,求实数k的取值范围;
是单调函数,求实数k的取值范围;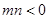 ,
,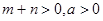 , 且
, 且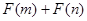 能否大于零?
能否大于零?